现在, 在动力传动用齿轮中使用最为广泛的齿形是渐开线齿形。
渐开线齿轮的特点是制作容易, 中心距多少有些误差也能圆滑地啮合。
3.1 渐开线齿轮的齿形及尺寸
图3.1 显示了渐开线齿轮齿形的基准齿条齿形。表3.1列出了有关齿形的术语、代号、计算公式及定义。如图所示的齿轮齿形, 齿高为模数的2.25 倍, 被称为全齿高齿。全齿高齿是最为一般的齿形。另外, 还有齿高低于全高齿的短齿齿形和齿高高于全高齿的高齿齿形。压力角为20 度的齿形最为常见。此外还有14.5 度、17.5 度等使用特殊压力角的齿轮。
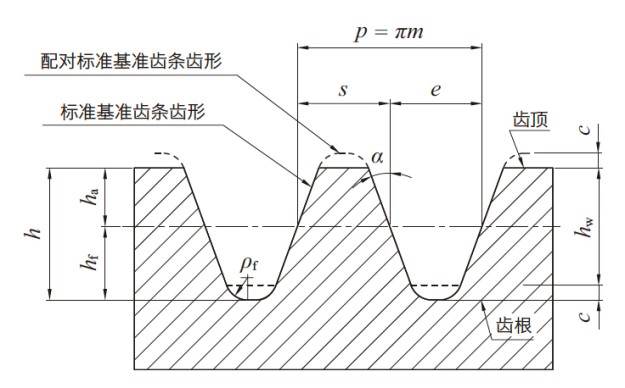
图3.1 基准齿条齿形
表3.1 有关齿形的术语| 术语 | 代号 | 公式 | 定义 |
| 模数 | m | p / π | 用公制单位表示轮齿大小的术语数值为分度圆齿距除以圆周率π |
| 齿距 | p | πm | 基准线上相邻两齿之间的距离模数m 与圆周率(π) 相乘之积 |
| 压力角 | α | （20 度） | 轮齿相对于基准线的法线的倾斜角度 |
| 齿顶高 | ha | 1.00m | 由基准线到齿顶的距离 |
| 齿根高 | hf | 1.25m | 由基准线到齿根的距离 |
| 齿高 | h | 2.25m | 齿顶到齿根的距离 |
| 工作齿高 | hw | 2.00m | 配对齿轮啮合的齿高 |
| 顶隙 | c | 0.25m | 齿高到配对齿轮的齿顶间的距离(间隙) |
| 齿根圆角半径 | ρf | 0.38m | 齿面与齿根间的曲率半径 |
JIS 标准中规定的一般机械及重机械用正齿轮及斜齿齿轮使用模数的标准值列于表3.2。标准推荐应尽量使用Ⅰ列的模数值并且避免使用模数6.5。
表3.2 模数标准值 / 单位mm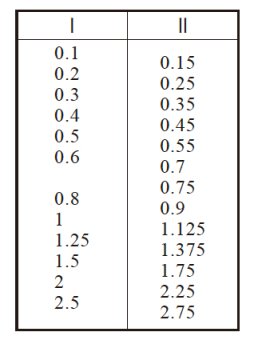
※摘自JIS B 1701-2: 1999 圆柱齿轮－渐开线齿轮
齿形第２部：模数
图3.2 示意了模数1 - 10 的齿条原尺。
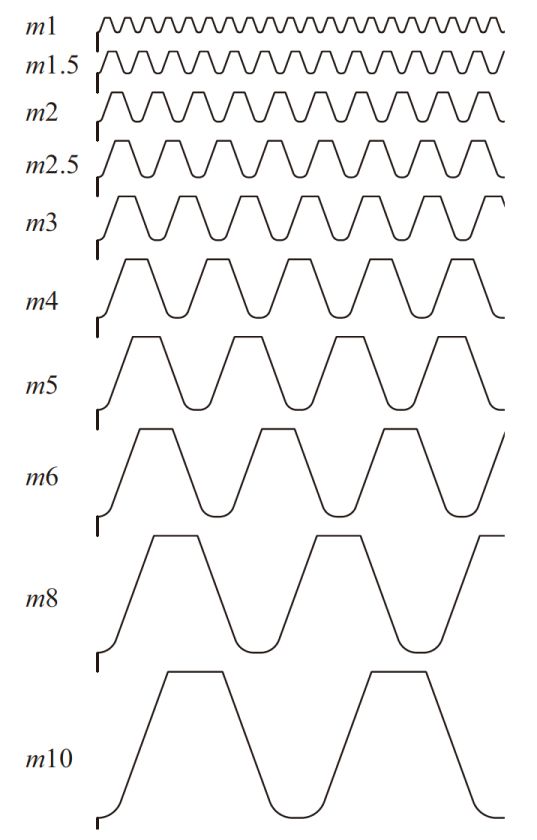
图3.2 齿条齿形的模数原寸图
除模数以外还有使用周节 p(CP) 或径节 P 来表示轮齿大小的方法。
周节(CP) 是指分度圆齿距p 。因为分度圆齿距为整数, 所以将其使用在进给机构中的话, 进给量可以简单的控制为整数。
径节 P(DP) 是长度单位使用英制单位的国家( 例如美国等) 所使用的表示轮齿大小的单位。径节P 可以通过公式(3.1) 与模数 m 进行换算。
m = 25.4 / P（3.1）
表3.3 是模数(m)、周节(CP）及径节(DP) 的对照表。
表3.3 齿距比较表| 模数 m |
周节 CP |
径节 DP |
| 0.39688 | 1.24682 | 64 |
| 0.5 | 1.57080 | 50.8 |
| 0.52917 | 1.66243 | 48 |
| 0.6 | 1.88496 | 42.33333 |
| 0.79375 | 2.49364 | 32 |
| 0.79577 | 2.5 | 31.91858 |
| 0.8 | 2.51327 | 31.75 |
| 1 | 3.14159 | 25.4 |
| 1.05833 | 3.32485 | 24 |
| 1.25 | 3.92699 | 20.32 |
| 1.27000 | 3.98982 | 20 |
| 1.5 | 4.71239 | 16.93333 |
| 1.59155 | 5 | 15.95929 |
| 1.58750 | 4.98728 | 16 |
| 2 | 6.28319 | 12.7 |
| 2.11667 | 6.64970 | 12 |
| 2.5 | 7.85398 | 10.16 |
| 2.54000 | 7.97965 | 10 |
| 3 | 9.42478 | 8.46667 |
| 3.17500 | 9.97456 | 8 |
| 3.18310 | 10 | 7.97965 |
| 4 | 12.56637 | 6.35 |
| 4.23333 | 13.29941 | 6 |
| 4.77465 | 15 | 5.31976 |
| 5 | 15.70796 | 5.08 |
| 5.08000 | 15.95929 | 5 |
| 6 | 18.84956 | 4.23333 |
| 6.35000 | 19.94911 | 4 |
| 6.36620 | 20 | 3.98982 |
| 8 | 25.13274 | 3.175 |
| 8.46667 | 26.59882 | 3 |
| 10 | 31.41593 | 2.54 |
3.2 渐开线曲线
如图3.3 所示, 渐开线曲线是一端固定在圆筒上的线,通过张力反松卷线时, 线的另一端所画出的曲线。这个圆筒是齿轮的基圆。沿着这个基圆转动规尺, 规尺上的一点所画出的曲线也为渐开线。
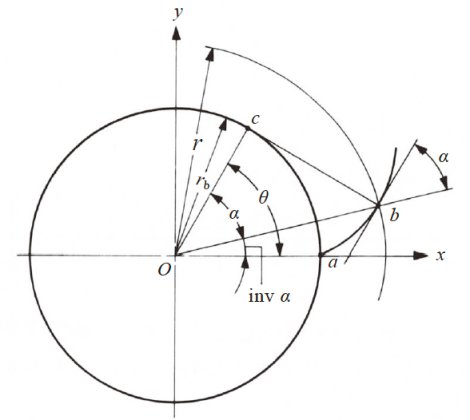
图3.3 渐开线曲线
图3.3 的invα 被称为渐开线函数角。单位为弧度( rad )。角度θ 则被称为渐开线转动角。
inv α = tan α − α ( rad ) （3.2）
渐开线曲线的( x , y ) 可根据公式(3.3) 进行计算。座标 的计算例列于表3.4 中。
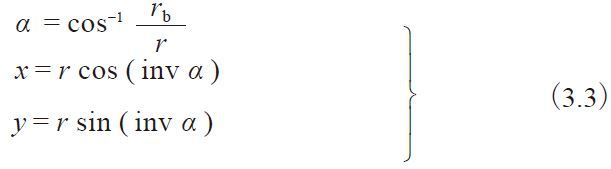表3.4 渐开线曲线座标计算例
| 齿轮要素 | 设定值 | 齿轮要素 | 设定值 |
| 模数 | 5 | 分度圆直径 | 150.00000 |
| 压力角 | 20 | 基圆直径 | 140.95389 |
| 齿数 | 30 | 齿顶圆直径 | 160 |
| r （半径） | α（压力角） | x 座标 | y 座标 |
| 70.47695 | 0.00000 | 70.4769 | 0.0000 |
| 72 | 11.80586 | 71.9997 | 0.2136 |
| 74 | 17.75087 | 73.9961 | 0.7628 |
| 76 | 21.97791 | 75.9848 | 1.5192 |
| 78 | 25.37123 | 77.9615 | 2.4494 |
| 80 | 28.24139 | 79.9218 | 3.5365 |
座标计算的顺序如下。
1. 决定半径 ( r )
2. 代入公式3.3, 分别计算出压力角及座标α、x / y
3.3 渐开线齿轮的啮合
图3.4 所示为一对标准正齿轮的啮合状态。
如图所示, 渐开线齿轮的接触点在基圆的公用切线( 作用线) 上移动。
由此得出, 做为一对齿轮的啮合条件, 基圆齿距pb必须相等。
pb = πm cos α （3.4）
通过公式(3.4) 可以看出, 一对齿轮啮合的条件不仅仅是模数m 相等, 压力角α 也必须相等, 齿轮才能正确地啮合。
图3.4 中作用线上的长度ab 被称为啮合线长度。
啮合线长度ab 除以基圆齿距pb 的值被称为端面重合度。
要想使齿轮做正确的传动, 重合度必须大于1。
如上所述, 渐开线齿轮啮合时, 模数m 和压力角α是十分重要的要素。
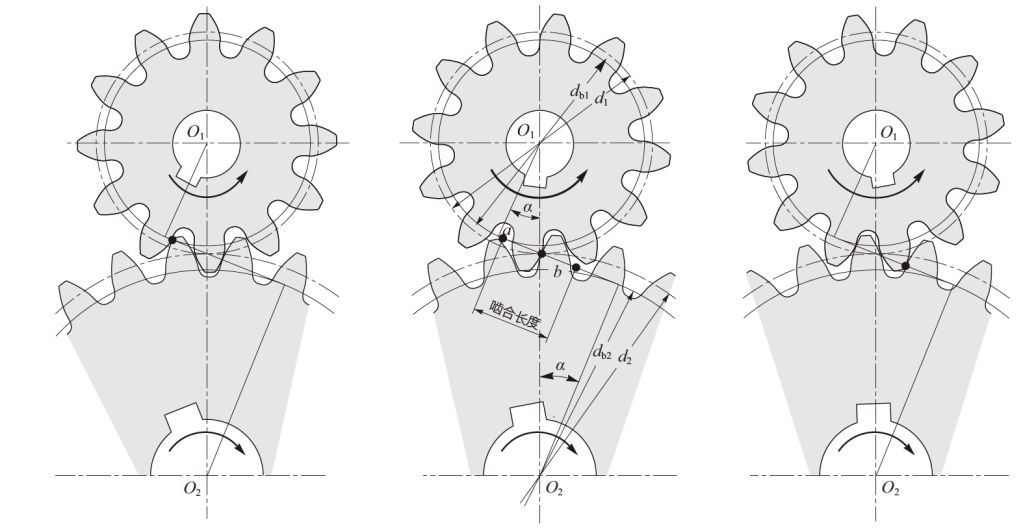
图3.4 渐开线齿轮的啮合
3.4 渐开线齿形的展成
利用齿条形刀具可以很容易地加工出渐开线齿形。
应用展成原理的切齿机械, 具有代表性的有滚齿机及插齿机。
图3.5 示意了利用展成机械加工渐开线齿形时的模样。做为标准正齿轮, 齿轮的分度圆直径和齿条形刀具的分度圆齿距线在不产生滑动的条件下相切转动,即可展成出如图3.5 所示的渐开线齿形。
做为渐开线齿轮的展成切削机械, 还有使用小齿轮铣刀的插齿机。这种插齿机, 不但可以加工外齿轮,还可以加工内齿轮
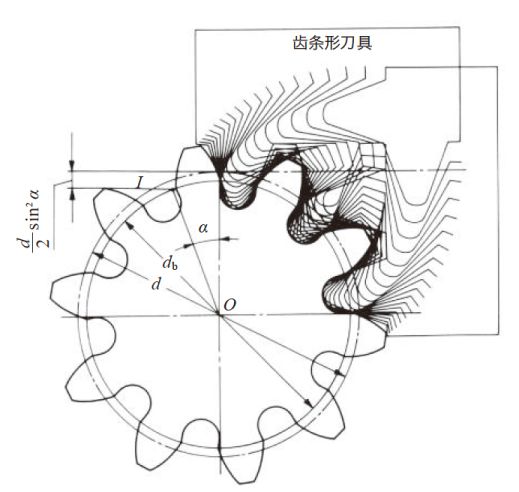
图3.5 标准正齿轮的展成(α = 20°, z = 10, x = 0 )
3.5 根切
如图3.5 中所示的小齿数正齿轮切齿加工时, 刀具超过根切界限点I 切削时, 产生根切。
根切是刀具的刃部先端直线部分（hc）将齿轮的齿根部齿形曲线的一部分切掉的现象。
设标准正齿轮的刀刃先端直线部的深度为m 话, 不产生根切的条件为:
根据这个条件, 导出标准正齿轮根切界限齿数z 的公 式（3.7)。
分度圆压力角α ＝ 20°时, 根切界限齿数z 为17.1。 不过, 即使齿数在17 以下, 强度及重合度等方面没有 问题的话, 在使用上没有妨碍。
3.6 齿轮的变位
图3.5 中所示的分度压力角α = 20°、齿数z = 10 的标准正齿轮发生根切。防止根切的方法是对齿轮实行变位。变位有正变位和负变位。为了防止如图3.5 中所示的根切, 我们列举了正变位的例子, 并图示于3.6 中。与图3.6 相反, 负变位的例子示意在图3.7 中。从图中可以明显地看出, 由于实行了负变位, 根切现象也变得更加严重了。图3.6 和图3.7 的变位齿轮加工时, 刀具的移动距离xm 被称为变位量, x 是变位系数。
变位齿轮不产生根切的条件是:
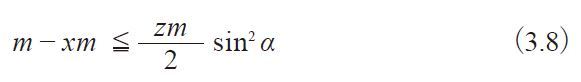表3.5 正齿轮齿顶宽度( 齿顶厚) 的计算
| 序号 | 项目 | 代号 | 单位 | 计算公式 | 计算例 | 1 | 模数 | m | mm | 设定值 | 2 |
| 2 | 压力角 | α | 度 | 20 | |
| 3 | 齿数 | z | - | 16 | |
| 4 | 变位系数 | x | - | 0.3 | |
| 5 | 分度圆直径 | d | mm | zm | 32 |
| 6 | 基圆直径 | db | dcosα | 30.07016 | |
| 7 | 齿顶圆直径 | da | d + 2m (1+ x) | 37.2 | |
| 8 | 齿顶圆压力角 | αa | 度 | cos-1 db / da | 36.06616 |
| 9 | 渐开线函数α | invα | 弧度 | tanα − α | 0.014904 |
| 10 | 渐开线函数αa | invαa | tanαa − αa | 0.098835 | |
| 11 | 齿顶圆齿厚半角 | ψa | π / 2z + 2x tan α / z + (invα - invαa) | 0.027893 | |
| 12 | 齿顶厚 | sa | mm | ψa da | 1.03762 |
由此得出根切界限齿数z 为:
同样亦可得出, 变位系数x 为:
除了防止根切的发生外, 调整中心距时, 也经常使用齿轮的变位。
齿轮在变位时必须注意的问题是齿顶的宽度。小齿数齿轮的正变位过大, 会造成齿顶过尖。
有关正齿轮齿顶宽度( 齿顶厚) 的计算方法列于表3.5中。
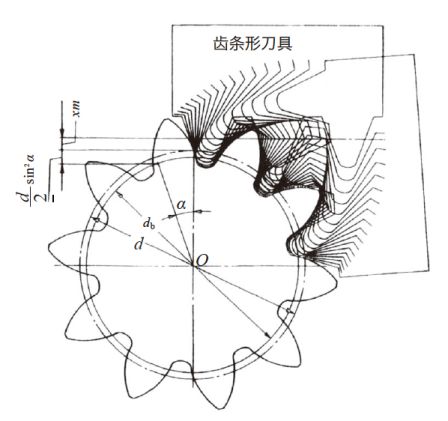
图3.6 正变位正齿轮的展成( α = 20°, z = 10, x = + 0.5 )
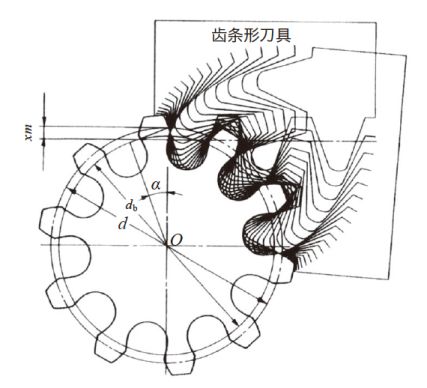
图3.7 负变位正齿轮的展成( α = 20°, z = 10, x = − 0.5 )
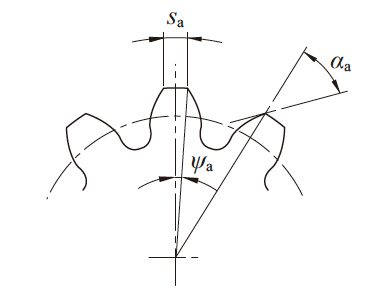
图3.8 齿顶厚
3.7 齿形修整及齿线修整
齿轮有许多特殊术语。齿轮加工也使用很多独特的方法。在这里我们将介绍其中具有代表性的方法。
（1）齿形修整
齿形修整是修缘和修根的总称。
一般地说, 修缘的方法使用比较普遍。
修缘是指有意识的修削齿顶的齿形, 使齿型偏离正确的渐开线齿形。
由此, 当齿轮齿面受外力产生变形时, 可以避免对与之啮合的齿轮产生干涉, 并且可以降低噪音, 延长齿轮寿命。
但是, 要注意不能修整过量。过量修整等于增加了齿形误差, 将对
啮合产生不良影响。
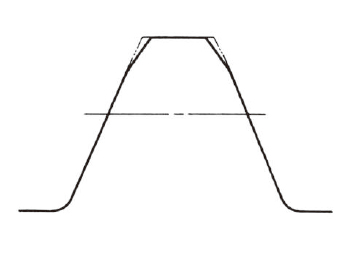
图3.9 齿形修整
（2）鼓形加工和齿端修薄
鼓形加工和齿端修薄都是沿齿线方向的修整。特别是鼓形加工, 是以使轮齿接触集中到齿宽的中央部为目的的加工, 所以, 沿齿线方向加工适当的鼓形。此时,应注意不能加工过甚。过量的鼓形加工会引起轮齿接触面积的减小, 对齿轮强度产生不良影响。
齿端修薄是将齿宽的两端部加以适当的倒角加工的方法。
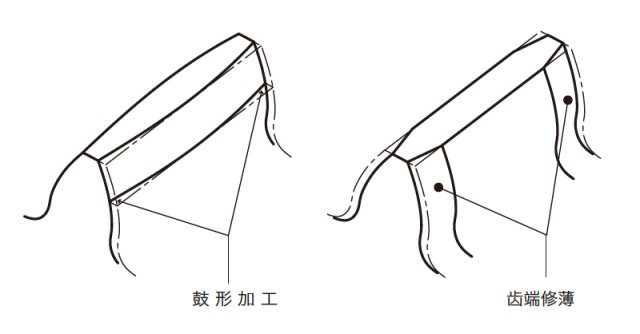
图3.10 鼓形加工和齿端修薄
（3）外径加工及齿顶倒角加工
使用滚齿展成法加工齿轮的方法, 已经在齿轮入门篇的3.4, 渐开线齿轮的展成中加以说明。滚齿加工的同时,齿轮的外径加工及齿顶倒角加工亦可同时进行。
图3.5、图3.6、图3.7 示意了利用齿条刀具进行齿形展成加工和外径加工的情形。通过这种加工, 可以减少外径的偏差, 还可以防止齿顶产生毛边。
图3.11 示意了齿顶倒角刀具的刀刃形状及由此刀具切削加工的齿轮齿形。通过齿顶倒角加工、对防止发生在齿顶的撞痕及毛刺等起了很好的作用。
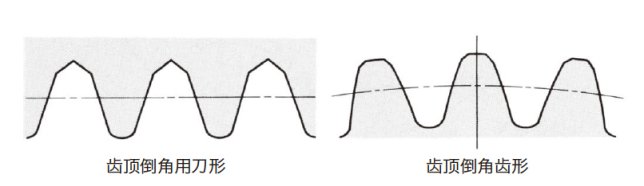
图3.11 齿顶倒角的刀形及齿形
因为实行了齿顶倒角, 啮合时有效的齿顶高减少, 啮合率也降低, 所以, 通常不希望过量的倒角。
图3.12 示意了标准的齿顶倒角的大小及形状。
外径加工及齿顶倒角有时并用, 有时单独采取其中的一种。
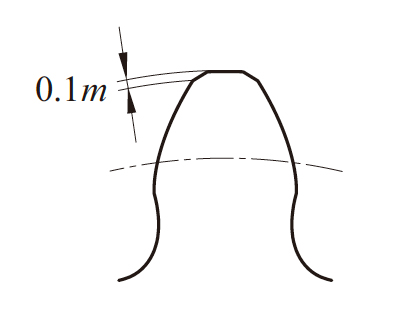
图3.12 齿顶倒角的大小及形状