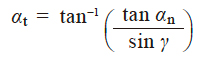不知道如何选择KHK标准齿轮 ？我们可以给您建议，请联系我们邮箱：info@khkchilun.com | 电话：(0371) 8615 1014 / 15713836720

齿轮的齿厚

齿轮的齿厚测定方法有二种, 一种是直接测齿厚,另一种是测与齿厚有关的其他尺寸。
一般采用弦齿厚法, 公法线长度法, 量柱( 球) 法。

5.1 弦齿厚法

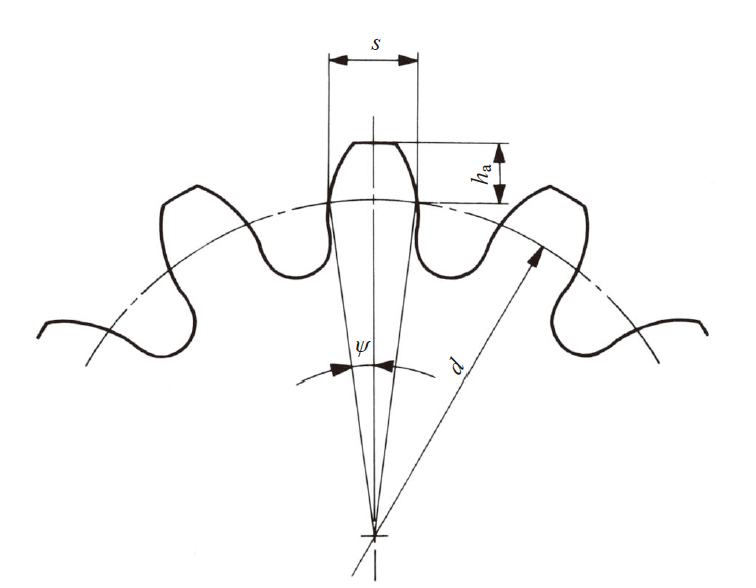
如图5.1 所示, 将齿轮的齿顶圆做为基准, 用卡钳测量分度圆上的弦齿厚。

（1）正齿轮

表5.1 为正齿轮的弦齿厚计算公式。

图4.1 标准正齿轮的啮合
图5.1 弦齿厚法 表5.1 正齿轮的弦齿厚
序号 计算项目 代号 计算方程式 计算例
1 圆弧齿厚 s
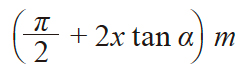
表5.1内 公式
m = 10
α = 20°
z = 12
x = +0.3
ha = 13.000
s = 17.8918
ψ = 8.54270°
s = 17.8256
ha = 13.6657
2 齿厚半角 ψ
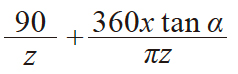
表5.1内 公式
3 弦齿厚 s̄ zm sin ψ
4 弦齿高 h̄a
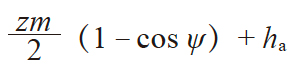
表5.1内 公式

（2）齿条和斜齿齿条

因为齿条的齿形为直线型, 所以使用的计算公式也很简单, 见表5.2。

表5.2 齿条的弦齿厚
序号 计算项目 代号 计算方程式 计算例
1 弦齿厚 s̄ πm / 2 或 πmn / 2 m = 3
α = 20°
s̄ = 4.7124
ha = 3.0000
2 弦齿高 h̄a ha

斜齿齿条亦可使用上表的公式进行计算。

（3）斜齿齿轮

弦齿厚在法平面上测定。
表5.3 是齿直角方式斜齿齿轮的计算表。表5.4 是轴直角方式斜齿齿轮的计算表。

表5.3 齿直角方式斜齿齿轮的弦齿厚
序号 计算项目 代号 计算方程式 计算例
1 法向齿厚 sn
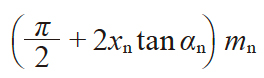
表5.3内 公式
mn = 5
αn = 20°
β = 25° 00' 00''
z = 16
xn = +0.2
ha = 6.0000
sn = 8.5819
zv = 21.4928
ψv = 4.57556°
s̄ = 8.5728
h̄a = 6.1712
2 当量齿轮齿数 zv
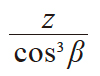
表5.3内 公式
3 齿厚半角 ψv
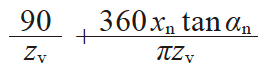
表5.3内 公式
4 弦齿厚 s̄ zvmn sin ψv
5 弦齿高 h̄a
表5.3内 公式
表5.4 轴直角方式斜齿齿轮的弦齿厚
序号 计算项目 代号 计算方程式 计算例
1 法向齿厚 sn
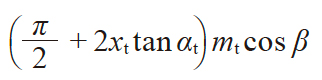
表5.4内 公式
mt = 2.5
αt = 20°
β = 21° 30' 00''
z = 20
xt = 0
ha = 2.5
sn = 3.6537
zv = 24.8311
ψv = 3.62448°
s̄ = 3.6513
h̄a = 2.5578
2 当量齿轮齿数 zv
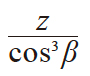
表5.4内 公式
3 齿厚半角 ψv
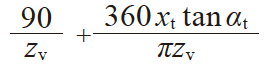
表5.4内 公式
4 弦齿厚 s̄ zv mt cos β sin ψv
5 弦齿高 h̄a
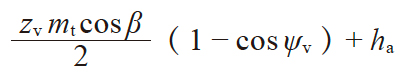
表5.4内 公式

（4）锥齿轮

表5.5 是格里森直齿锥齿轮的计算表, 表5.6 是标准直齿锥齿轮的计算表, 表5.7 是格里森弧齿锥齿轮的计算表。
表中的弦齿高的计算公式为近似公式。

表5.5 格里森直齿锥齿轮的弦齿厚
序号 计算项目 代号 计算方程式 计算例
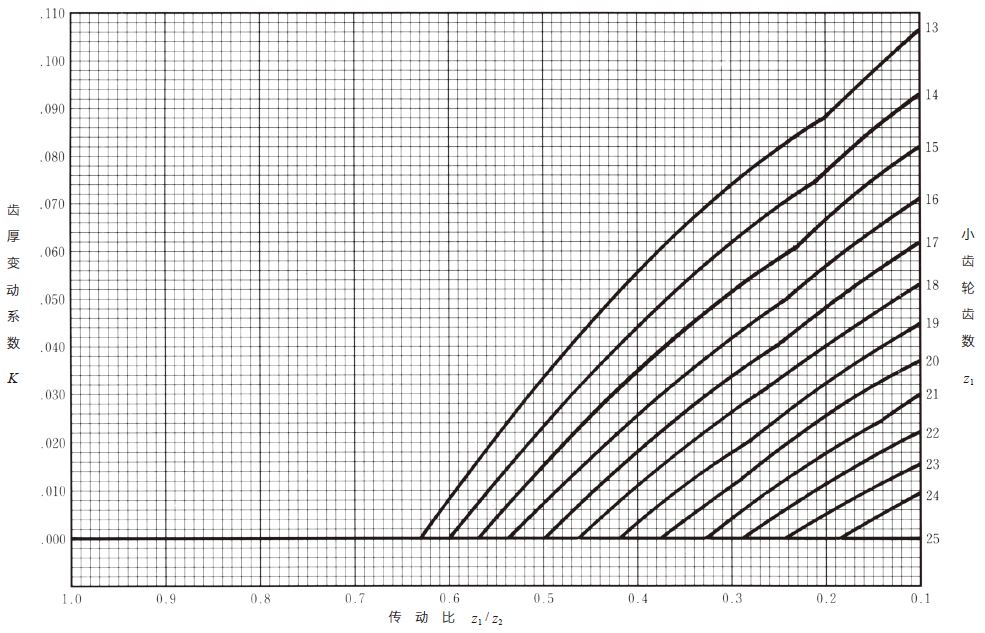
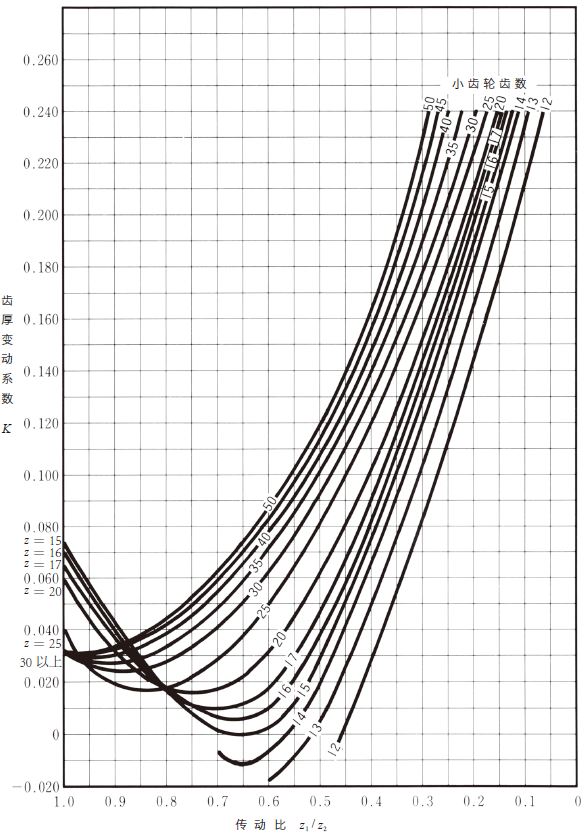
1 齿厚变动系数
(切向变位系数)		 K 由图5.2 中求出。
m = 4
α = 20°
Σ = 90°
z1= 16 z2 = 40
z1 /z2 = 0.4
K = 0.0259
ha1 = 5.5456 ha2 = 2.4544
δ1 = 21.8014° δ2 = 68.1986°
s1 = 7.5119 s2 = 5.0545
s̄1 = 7.4946 s̄2 = 5.0536
h̄a1 = 5.7502 h̄a2 = 2.4692
2 齿厚 s1
s2		 πm − s2
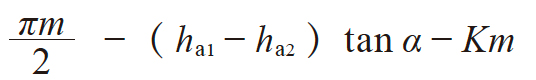
表5.5内 公式
3 弦齿厚 s̄
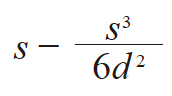
表5.5内 公式
4 弦齿高 h̄a
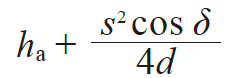
表5.5内 公式
图5.2 格里森直齿锥齿轮的齿厚变动系数K 线图
图5.2 格里森直齿锥齿轮的齿厚变动系数K 线图 表5.6 标准直齿锥齿轮的弦齿厚
序号 计算项目 代号 计算方程式 计算例
1 弧齿厚 s πm / 2
m = 4
α = 20°
Σ = 90°
z1= 16 z2 = 40
d1 = 64 d2 = 160
ha = 4.0000
δ1 = 21.8014° δ2 = 68.1986°
s = 6.2832
zv1 = 17.2325 zv2 = 107.7033
Rv1 = 34.4650 Rv2 = 215.4066
ψv1 = 5.2227° ψv2 = 0.83563°
s̄1 = 6.2745 s̄2 = 6.2830
h̄a1 = 4.1431 h̄a2 = 4.0229
2 当量齿轮齿数 zv
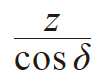
表5.6内 公式
3 背锥距 Rv
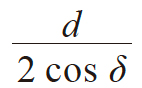
表5.6内 公式
4 齿厚半角 ψv 90 / zv
5 弦齿厚 s̄ zv m sin ψv
6 弦齿厚 h̄a ha + Rv（ 1 − cos ψv ）

直齿锥齿轮在使用格里森刨齿机切齿时, 有必要计算刨齿机用的齿角
计算公式如(5.1) 所示。

公式 5.1

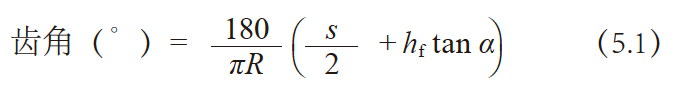
这个角度是为了决定直齿锥齿轮的弧齿厚s 而设置的, 只为参考值。

图5.3 格里森弧齿锥齿轮的齿厚变动系数K 线图
图5.3 格里森弧齿锥齿轮的齿厚变动系数K 线图 表5.7 格里森弧齿锥齿轮
序号 计算项目 代号 计算方程式 计算例
1 齿厚变动系数 K 由图5.3 中求出。
Σ = 90° m = 3 αn = 20°
z1 = 20 z2 = 40 βm = 35°
ha1= 3.4275 ha2= 1.6725
K = 0.060
p = 9.4248
s1 = 5.6722 s2 = 3.7526
2 齿厚 s1
s2		 p − s2
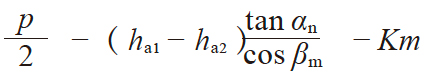
表5.7内 公式

弦齿厚的计算公式, 随切齿方式而变化, 计算亦非常复杂, 在这里加以省略。

（5）蜗杆蜗轮

表5.8 是轴向模数方式蜗杆副的计算表, 表5.9 是齿直角方式蜗杆副的计算表。

表5.8 轴向模数方式蜗杆副
序号 计算项目 代号 计算方程式 计算例
1 轴向齿厚(蜗杆)
端面齿厚(蜗轮)		 sx1
st2		 πmx / 2
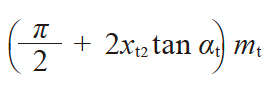
表5.8内 公式
mx = 3 mt = 3
αn = 20°
z1 = 2 z2 = 30
d1 = 38 d2 = 90
a = 65
xt2 = +0.33333
ha1 = 3.0000 ha2 = 4.0000
γ = 8.97263°
αt = 20.22780°
sx1 = 4.71239 st2 = 5.44934
zv2 = 31.12885
ψv2 = 3.34335°
s̄1 = 4.6547 s̄2 = 5.3796
h̄a1 = 3.0035 ha2 = 4.0785
2 当量齿轮齿数
（蜗轮）		 zv2
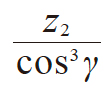
表5.8内 公式
3 齿厚半角
（蜗轮）		 ψv2
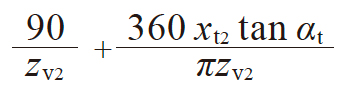
表5.8内 公式
4 弦齿厚 s̄1
s̄2		 sx1 cos γ
zv2 mt cos γ sin ψv2
5 弦齿高 h̄a1
h̄a2
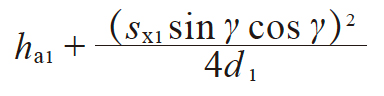
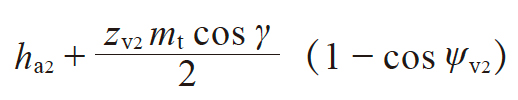
表5.8内 公式
表5.8内 公式
表5.9 齿直角方式蜗杆副
序号 计算项目 代号 计算方程式 计算例
1 法向齿厚 sn1
sn2		 πmn / 2
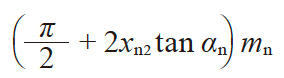
表5.9内 公式
mn = 3
αn = 20°
z1 = 2 z2 = 30
d1 = 38 d2 = 91.1433
a = 65
xn2 = 0.14278
ha1 = 3.0000 ha2 = 3.42835
γ = 9.08472°
sn1 = 4.71239 sn2 = 5.02419
zv2 = 31.15789
ψv2 = 3.07964°
s̄1 = 4.7124 s̄2 = 5.0218
h̄a1 = 3.0036 ha2 = 3.4958
2 当量齿轮齿数
（蜗轮）		 zv2 z2 / cos3 γ
3 齿厚半角
（蜗轮）		 ψv2
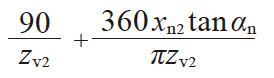
表5.9内 公式
4 弦齿厚 s̄1
s̄2		 sn1
zv2 mn sin ψv2
5 弦齿高 h̄a1
h̄a2
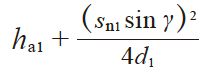
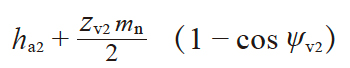
表5.9内 公式
表5.9内 公式

5.2 公法线长度法

如图5.4 所示, 使用卡尺测定跨齿数为 k 的公法线长度 W , 卡爪相切于轮齿的不同侧面。用这个方法所测出的公法线长度是基圆柱上的法向齿厚 sbn 与基圆齿距 pbn ×（k － 1）的和。

（1）正齿轮与内齿轮

表5.10 列出了计算公式。

表5.10 正齿轮及内齿轮的公法线长度
序号 计算项目 代号 计算方程式 计算例
1 跨齿数 k kth = zK（ f ）+ 0.5
k 是与kth 最接近的整数。 注1 		m = 3
α = 20°
z = 24
x = +0.4
kth = 3.78787
k = 4
W = 32.8266
2 公法线长度 W
m cos α {π（k − 0.5）+ z inv α} + 2 xm sin α + 2 xm sin α

注1. 其中

公式 5.2

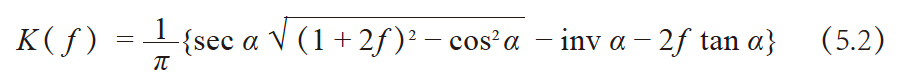
f = x / z

图5.4 示意了正齿轮的公法线长度测定法, 测量轮齿的外侧尺寸。
内齿轮的齿形, 因为是正齿轮的齿槽部分为轮齿,所以, 内齿轮的公法线测定时与正齿轮相反, 在齿的内测进行测量。

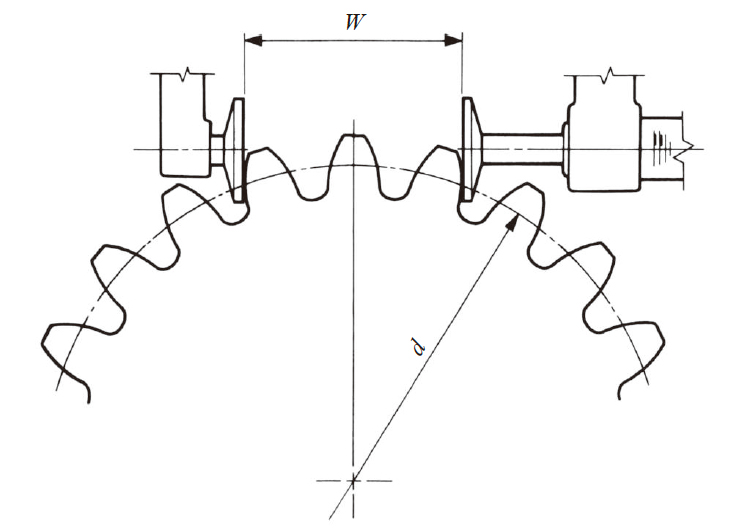
图5.4 公法线长度法（正齿轮）
图5.4 公法线长度法（正齿轮）

（2）斜齿齿轮

表5.11 是齿直角方式斜齿齿轮的计算表, 表5.12 是轴直角方式斜齿齿轮的计算表。

表5.11 齿直角方式斜齿齿轮的公法线长度
序号 计算项目 代号 计算方程式 计算例
1 跨齿数 k kth = zK（ f ）+ 0.5
k 是与kth 最接近的整数。 注1 		mn = 3, αn= 20°, z = 24
β = 25°00' 00''
xn = +0.4
αt = 21.88023°
kth = 4.63009
k = 5
W = 42.0085
2 公法线长度 W
mn cos αn {π（k − 0.5）+ z inv αt } + 2xnmn sin αn
注1. 其中

公式 5.3

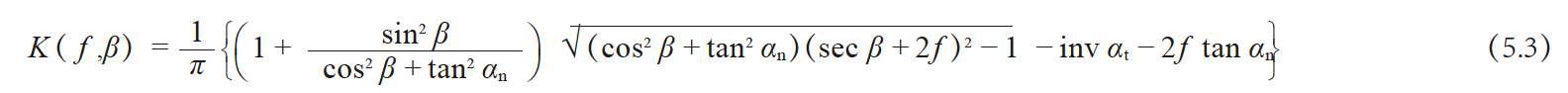
只是　f = xn / z

变位正齿轮及斜齿齿轮的求跨齿数速查图登载在第609 页。

表5.12 轴直角方式斜齿齿轮的公法线长度
序号 计算项目 代号 计算方程式 计算例
1 跨齿数 k kth = zK（ f ）+ 0.5
k 是与kth 最接近的整数。 注1 		mt = 3, αt= 20°, z = 24
β = 22°30' 00''
xt = +0.4
αn = 18.58597°
kth = 4.31728
k = 4
W = 30.5910
2 公法线长度 W
mt cos β cos αn {π（k − 0.5）+ z inv αt} + 2 xt mt sin αn
注1. 其中

公式 5.4

f = xt / z cos β

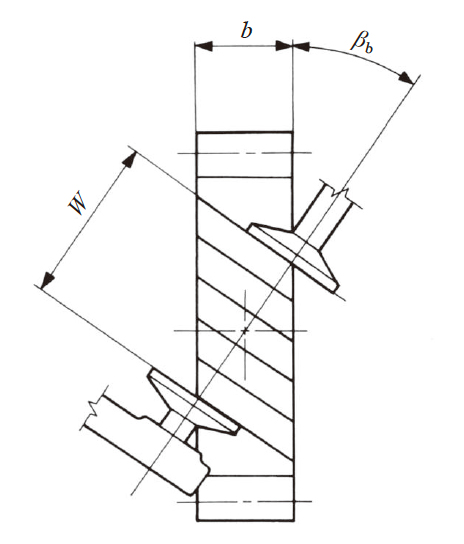
如图5.5 所示, 斜齿齿轮的公法线长度测定时, 需要有一定的齿宽( 端面宽度)。
如果设最低齿宽为 b min 的话:

b min = W sin βb + Δb（5.5）
其中 βb 是基圆螺旋角

公式 5.6

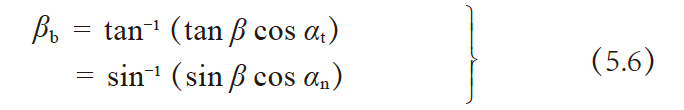
要想获得安定的测量数据, Δb 的量至少要取3mm左右。
标准正齿轮的公法线（压力角20 度及14.5 度）数据表登载在590 ～ 593 页。

图5.5 斜齿齿轮的齿宽
图5.5 斜齿齿轮的齿宽

5.3 量柱(球)法

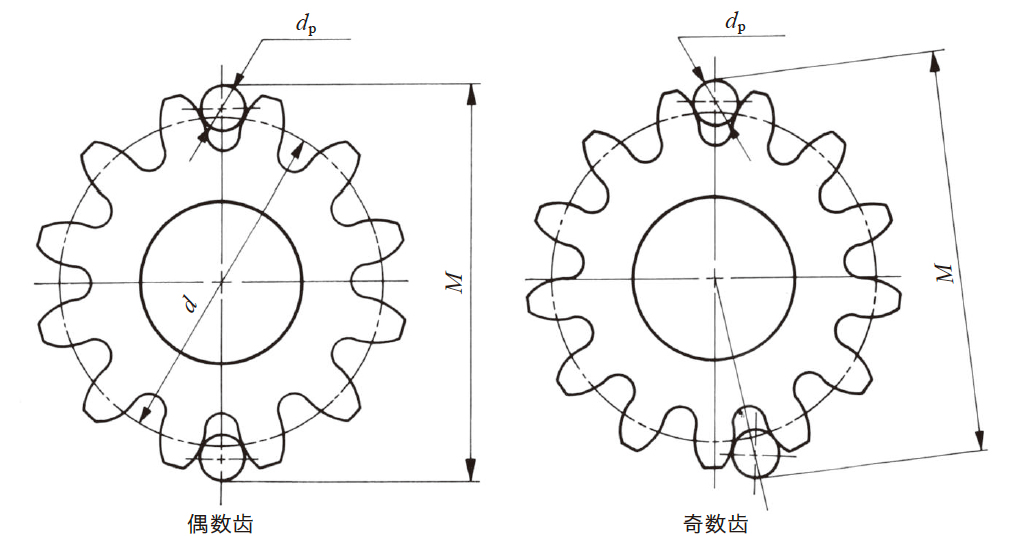
正齿轮及斜齿齿轮测定时, 如图5.6 所示。偶数齿时,量柱( 球) 放入沿直角方向相对应的两齿槽中, 奇数齿时, 将量柱( 球) 放入偏转180/z(° ) 角度的齿槽中,然后测定其外侧尺寸。
内齿轮时, 测量其内侧尺寸。
测定斜齿齿轮时, 使用两个量柱( 球)。

测定齿条时如图5.8 所示, 将量柱( 球) 放入到齿槽中, 用卡尺测量从基准面到量柱( 球) 的距离, 只需使用一个量柱( 球)。
测定蜗杆时, 如图5.10 所示, 将三根量柱放入齿槽中,测量其外侧尺寸。
这种方法称为三量柱法, 与螺丝的精密测定时使用的三针法相同。

图5.6 正齿轮的量柱(球)法
图5.6 正齿轮的量柱(球)法

（1）正齿轮

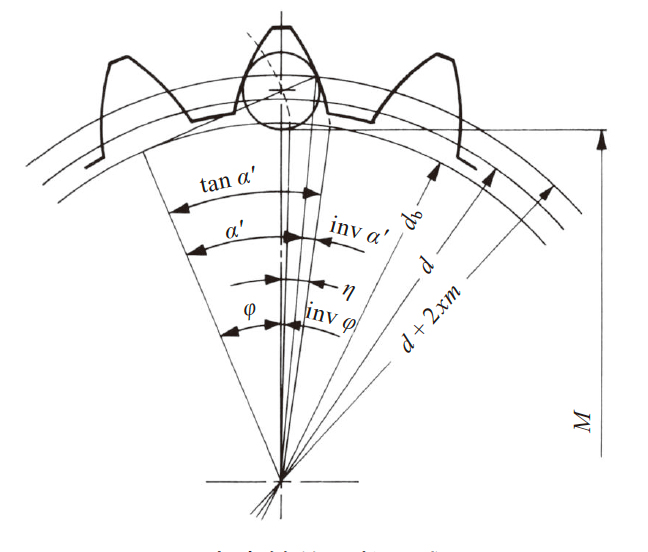
柱(球) 法的量柱(球), 标准齿轮时在啮合节圆上,变位齿轮时在 d ＋ 2xm 的圆上与齿轮相接触是最为理想的。
如图5.7 中所示的正齿轮中, 求出在理想齿面上的量柱(球) 直径的方法列于表5.13。

表5.13 与正齿轮接触的量柱(球)直径
序号 计算项目 代号 计算方程式 计算例
1 齿槽半角 η
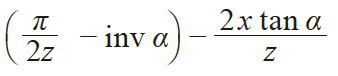
表5.13内 公式
m = 1
α = 20°
z = 20
x = 0
η = 0.0636354
α' = 20°
φ = 0.4276057
d'p = 1.7245
2 量柱(球)与齿面
接触点上的压力角		 α'
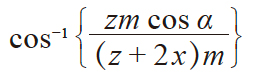
表5.13内 公式
3 通过量柱中心的作用角 φ tan α' + η
4 量柱(球)的理想直径 d'p zm cos α（inv φ + η）
注.角度η、φ 的单位为弧度。

这里所计算出的量柱( 球) 的直径为理想值, 需要特别制作, 才能得到手。
这种情况下, 使用与所计算的直径值相近, 在市场上出售的高精度量柱( 球) 进行测量才是比较现实的。
量柱的直径定下来后, 通过表5.14 进行量柱跨距计算。

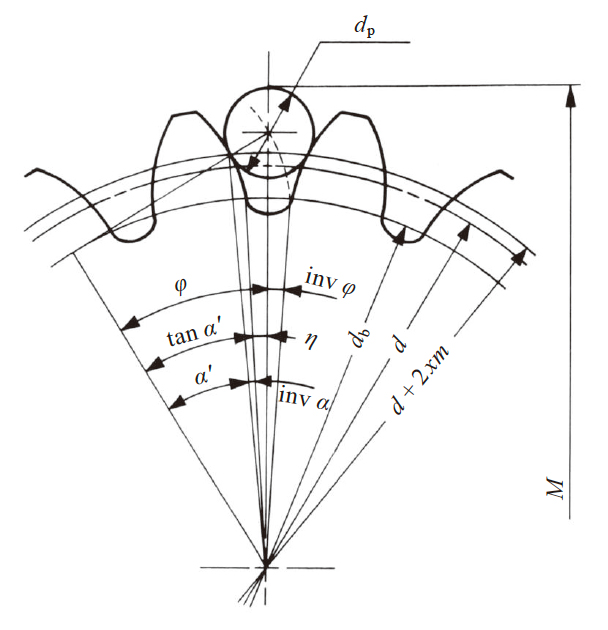
图5.7 正齿轮的量柱跨距
图5.7 正齿轮的量柱跨距 表5.14 正齿轮的量柱(球) 跨距
序号 计算项目 代号 计算方程式 计算例
1 量柱(球)直径 dp 注1 dp = 1.7(设定)
inv φ = 0.0268197
φ = 24.1350°
M = 22.2941
2 φ 的渐开线函数 inv φ
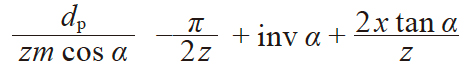
表5.14内 公式
3 通过量柱中心的作用角 φ 由渐开线函数表中查出。
4 量柱(球)跨距 M 偶数齿
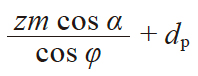
表5.14内 公式
奇数齿
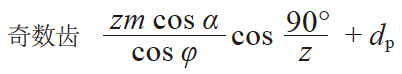
表5.14内 公式
注1. 使用由表5.13 所求出的理想量柱(球)直径或与之接近的直径。

表5.15 为模数 m ＝ 1, 分度圆压力角 α ＝ 20°的正齿轮在 d ＋ 2xm 的圆上与量柱( 球) 相接时, 量柱( 球) 的计算直径值。

表5.15　d+2xm 圆上与正齿轮相接的量柱(球)直径m = 1、α = 20°
齿数
z		 变位系数x
－0.4 －0.2 0 0.2 0.4 0.6 0.8 1.0
10 1.6347 1.7886 1.9979 2.2687 2.6079 3.0248 3.5315
20 1.6231 1.6599 1.7244 1.8149 1.9306 2.0718 2.2389 2.4329
30 1.6418 1.6649 1.7057 1.7632 1.8369 1.9267 2.0324 2.1542
40 1.6500 1.6669 1.6967 1.7389 1.7930 1.8589 1.9365 2.0257
50 1.6547 1.6680 1.6915 1.7247 1.7675 1.8196 1.8810 1.9515
60 1.6577 1.6687 1.6881 1.7155 1.7509 1.7940 1.8448 1.9032
70 1.6598 1.6692 1.6857 1.7090 1.7391 1.7759 1.8193 1.8691
80 1.6613 1.6695 1.6839 1.7042 1.7304 1.7625 1.8003 1.8438
90 1.6625 1.6698 1.6825 1.7005 1.7237 1.7521 1.7857 1.8242
100 1.6635 1.6700 1.6814 1.6975 1.7184 1.7439 1.7740 1.8087
110 1.6642 1.6701 1.6805 1.6951 1.7140 1.7372 1.7645 1.7960
120 1.6649 1.6703 1.6797 1.6931 1.7104 1.7316 1.7567 1.7855
130 1.6654 1.6704 1.6791 1.6914 1.7074 1.7269 1.7500 1.7766
140 1.6659 1.6705 1.6785 1.6900 1.7048 1.7229 1.7443 1.7690
150 1.6663 1.6706 1.6781 1.6887 1.7025 1.7194 1.7394 1.7625
160 1.6666 1.6706 1.6777 1.6876 1.7006 1.7164 1.7351 1.7567
170 1.6669 1.6707 1.6773 1.6867 1.6988 1.7137 1.7314 1.7517
180 1.6672 1.6707 1.6770 1.6858 1.6973 1.7114 1.7280 1.7472
190 1.6674 1.6708 1.6767 1.6851 1.6959 1.7093 1.7250 1.7432
200 1.6676 1.6708 1.6764 1.6844 1.6947 1.7074 1.7223 1.7396

（2）齿条与斜齿齿条

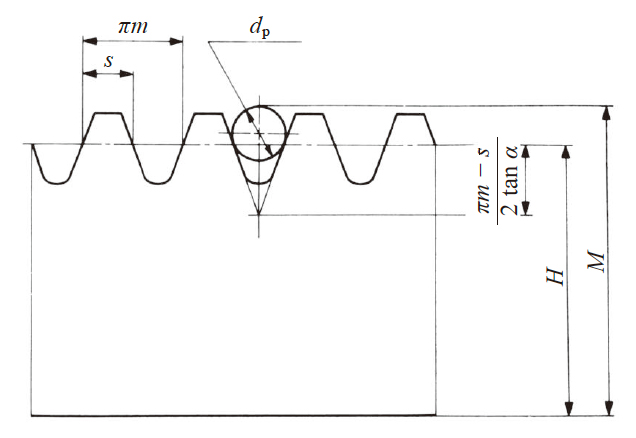
在齿条上, 量柱( 球) 与分度圆节线上相接是最为理想的。
齿条的量柱跨距计算列于表5.16。
斜齿齿条的情况下, 将表中的模数 m 换成法向模数 mn 分度圆压力角 α 换成法向压力角 αn 后进行计算。

图5.8 齿条的量柱跨距
图5.8 齿条的量柱跨距 表5.16A 齿条的量柱(球)跨距
序号 计算项目 代号 计算方程式 计算例
1 理想量柱(球)直径 d'p
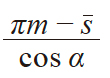
表5.16A内 公式
m = 1
α = 20°
s = 1.5708
d'p = 1.6716
dp = 1.7 (设定)
H = 14.0000
M = 15.1774
2 量柱(球)跨距 M
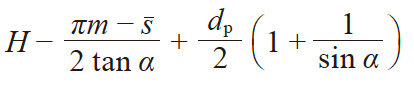
表5.16A内 公式
表5.16B 斜齿齿条的量柱(球)跨距
序号 计算项目 代号 计算方程式 计算例
1 理想量柱(球)直径 d'p
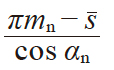
表5.16B内 公式
mn = 1
αn = 20°、β = 15°
s = 1.5708
d'p = 1.6716
dp = 1.7 (设定)
H = 14.0000
M = 15.1774
2 量柱(球)跨距 M
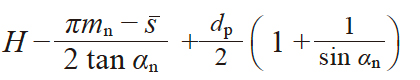
表5.16A内 公式

（3）内齿轮

如图5.9 所示, 内齿轮的情况下, 也是量柱(球)在 d ＋ 2xm 的圆上于内齿轮相接是最为理想的。
表5.17 是理想量柱( 球) 直径的求法计算表, 表5.18 是内齿轮的内侧量柱跨距计算表。

图5.9 内齿轮的量柱( 球) 跨距
图5.9 内齿轮的量柱( 球) 跨距 表5.17 量柱(球)的直径
序号 计算项目 代号 计算方程式 计算例
1 齿槽半角 η
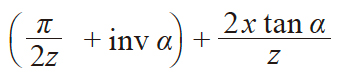
表5.17内 公式
m = 1
α = 20°
z = 40
x = 0
η = 0.054174
α' = 20°
φ = 0.309796
d'p = 1.6489
2 量柱(球)与齿面接触点
上的压力角		 α'
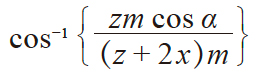
表5.17内 公式
3 通过量柱中心的压力角 φ tan α' − η
4 理想的量柱(球)直径 d'p zm cos α（η − inv φ）
注. 角度 ηv、φv的单位为弧度。 表5.18 内齿轮的量柱( 球) 内侧跨距
序号 计算项目 代号 计算方程式 计算例
1 量球(柱)的直径 dp 注1 dp = 1.7(设定)
inv φ = 0.0089467
φ = 16.9521°
M = 37.5951
2 φ 的渐开线函数 inv φ
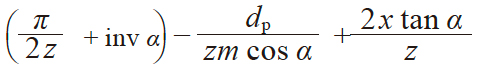
表5.18内 公式
3 通过量柱中心的作用角 φ 由渐开线函数表中查出。
4 量柱内侧跨距 M 偶数齿
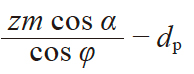
表5.18内 公式
奇数齿
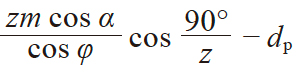
表5.18内 公式
注1. 使用通过表5.17 所求出的量柱(球)直径或与之接近的量柱直径。

表5.19 为模数 m ＝ 1, 分度圆压力角 α ＝ 20°的内齿轮在 d ＋ 2xm 的圆上与量柱(球) 相接时, 量柱(球)的计算直径值。

表 5.19 在 d +2xm圆上与内齿轮相接的量柱直径m = 1、α = 20°
齿数
z		 变位系数x
－0.4 －0.2 0 0.2 0.4 0.6 0.8 1.0
10 － 1.4789 1.5936 1.6758 1.7283 1.7519 1.7460 1.7092
20 1.4687 1.5604 1.6284 1.6759 1.7047 1.7154 1.7084 1.6837
30 1.5309 1.5942 1.6418 1.6751 1.6949 1.7016 1.6956 1.6771
40 1.5640 1.6123 1.6489 1.6745 1.6895 1.6944 1.6893 1.6744
50 1.5845 1.6236 1.6532 1.6740 1.6862 1.6900 1.6856 1.6732
60 1.5985 1.6312 1.6562 1.6737 1.6839 1.6870 1.6832 1.6725
70 1.6086 1.6368 1.6583 1.6734 1.6822 1.6849 1.6815 1.6721
80 1.6162 1.6410 1.6600 1.6732 1.6810 1.6833 1.6802 1.6718
90 1.6222 1.6443 1.6612 1.6731 1.6800 1.6820 1.6792 1.6717
100 1.6270 1.6470 1.6622 1.6729 1.6792 1.6810 1.6784 1.6715
110 1.6310 1.6492 1.6631 1.6728 1.6785 1.6801 1.6778 1.6715
120 1.6343 1.6510 1.6638 1.6727 1.6779 1.6794 1.6772 1.6714
130 1.6371 1.6525 1.6644 1.6727 1.6775 1.6788 1.6768 1.6714
140 1.6395 1.6539 1.6649 1.6726 1.6771 1.6783 1.6764 1.6714
150 1.6416 1.6550 1.6653 1.6725 1.6767 1.6779 1.6761 1.6713
160 1.6435 1.6561 1.6657 1.6725 1.6764 1.6775 1.6758 1.6713
170 1.6451 1.6570 1.6661 1.6724 1.6761 1.6771 1.6755 1.6713
180 1.6466 1.6578 1.6664 1.6724 1.6759 1.6768 1.6753 1.6713
190 1.6479 1.6585 1.6666 1.6723 1.6757 1.6766 1.6751 1.6713
200 1.6490 1.6591 1.6669 1.6723 1.6755 1.6763 1.6749 1.6713

（4）斜齿齿轮

斜齿齿轮上, 在 d ＋ 2xn mn 圆上与齿轮相接的理想量柱(球) 直径, 利用正齿轮的公式, 将式中的齿数 z 换成当量齿数 zv , 即可得到量柱直径的计算值。

表5.20 是齿直角方式斜齿齿轮的量球(柱)直径的计算表, 表5.21 是量球(柱)跨距的计算表。

表5.20 齿直角方式斜齿齿轮的量球(柱) 直径
序号 计算项目 代号 计算方程式 计算例
1 当量齿轮齿数 zv
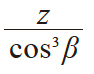
表5.20内 公式
mn = 1
αn = 20°
z = 20
β = 15°00' 00''
xn = +0.4
zv = 22.19211
ηv = 0.0427566
α'v = 24.90647°
φv = 0.507078
d'p = 1.9020
2 齿槽半角 ηv
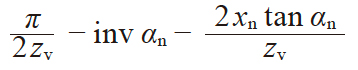
表5.20内 公式
3 量球(柱)与齿面
接点上的压力角		 α'v
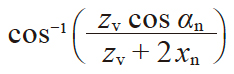
表5.20内 公式
4 过量球(柱)中心的压力角 φv tan α'v + ηv
5 理想的量球(柱)的直径 d'p zvmn cos αn（ inv φv + ηv ）
注. 角度ηv、φv 的单位为弧度。 表5.21 齿直角方式斜齿齿轮的量球(柱)跨距
序号 计算项目 代号 计算方程式 计算例
1 量柱(球)直径 dp 注1 dp = 2(设定)
αt = 20.646896°
inv φ = 0.058890
φ = 30.8534°
M = 24.5696
2 φ 的渐开线函数 inv φ
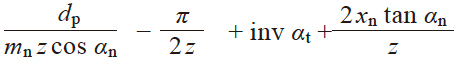
表5.21内 公式
3 通过中心的压力角 φ 由渐开线函数表中查出。
4 量球(柱)跨距 M 偶数齿
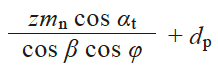
表5.21内 公式
奇数齿
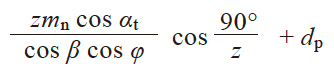
表5.21内 公式
注1. 使用通过表5.20 所求出的量球(柱)直径或与之接近的量球。

表5.22 是轴直角方式斜齿齿轮的量球( 柱) 直径的计算表, 表5.23 是量球(柱)跨距的计算表。

表5.22 轴直角方式斜齿齿轮的量球(柱)直径
序号 计算项目 代号 计算方程式 计算例
1 当量齿轮齿数 zv
表5.22内 公式
mt = 3
αt = 20°
z = 36
β = 33°33' 26.3''
αn = 16.87300°
xt = +0.2
zv = 62.20800
ηv = 0.014091
α'v = 18.26390
φv = 0.34411
inv φv = 0.014258
d'p = 4.2190
2 齿槽半角 ηv
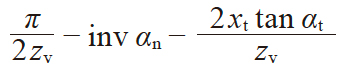
表5.22内 公式
3 量球( 柱) 与齿面
接点上的压力角		 α'v
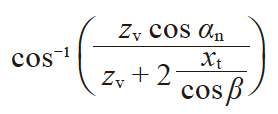
表5.22内 公式
4 通过量球(柱)中心的压力角 φv tan α'v + ηv
5 理想的量球(柱)的直径 d'p zv mt cos β cos αn（ inv φv + ηv ）
注. 角度ηv、φv 的单位为弧度。 表5.23 轴直角方式斜齿齿轮的量球(柱)跨距
序号 计算项目 代号 计算方程式 计算例
1 量球(柱)直径 dp 注1 dp = 4.5
inv φ = 0.027564
φ = 24.3453°
M = 115.892
2 φ 的渐开线函数 inv φ
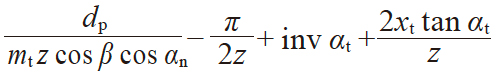
表5.23内 公式
3 通过球心的压力角 φ 由渐开线函数表中查出。
4 量球(柱)跨距 M 偶数齿
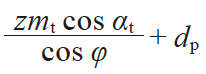
表5.23内 公式
奇数齿
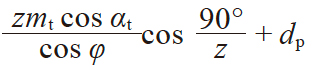
表5.23内 公式
注1. 使用通过表5.22 所求出的量球( 柱) 直径或与之接近的量球。

（5）蜗杆的三量柱法

做为蜗杆的齿形被广泛使用的３型齿形, 虽然以工具压力角 α0 ＝ 20°做为基准, 但是用此刀具切齿时,蜗杆的法向压力角 αn 将小于20° , 求出这个法向压力角 αn 的 AGMA( 美国齿轮制造商协会) 近似值的方程式如下所示。

公式 5.7

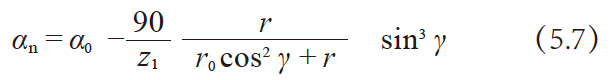
其中

r
：蜗杆的分度圆半径
r0
：刀具的半径
z1
：蜗杆的头数
γ
：蜗杆的分度圆柱导程角
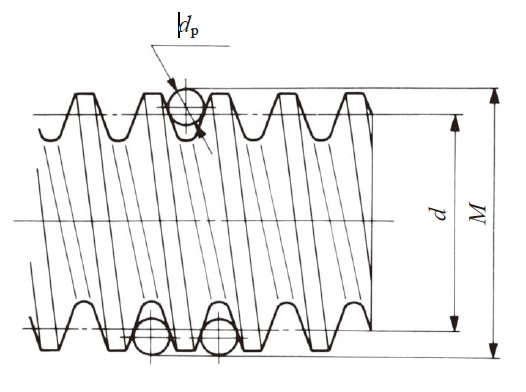
图5.10 蜗杆的三量柱法
图5.10 蜗杆的三量柱法

有关3 型齿形三量柱跨距的资料非常少, 在这里介绍几种近似的计算方法。

（a）将蜗杆看成与齿条相同的直线齿形进行计算

如果将蜗杆的齿形近似地看成直线齿形的话, 可以与齿条同样利用表5.24的方法进行计算。

表5.24 蜗杆的三量柱跨距的计算（a）－ 1
序号 计算项目 代号 计算方程式 计算例
1 理想的量柱(球)直径 d'p
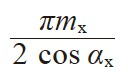
表5.24内 公式
mx = 2 αn = 20°
z1 = 1 d1 = 31
γ = 3.691386°
αx = 20.03827°
d'p = 3.3440
dp = 3.3
M = 35.3173
2 三量柱跨距 M
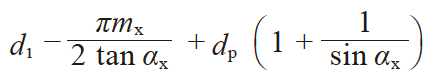
表5.24内 公式

但是, 这种方法中, 因为蜗杆的导程角很小, 所以没有加以考虑其影响。导程角变大时, 误差也将随之增加。
考虑导程角影响的计算方法列于表5.25。

表5.25 蜗杆的三量柱跨距的计算（a）－ 2
序号 计算项目 代号 计算方程式 计算例
1 理想的量柱(球)直径 d'p
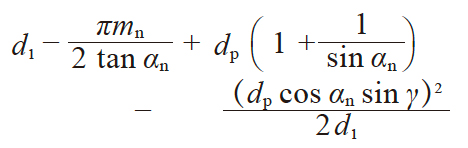
表5.25内 公式
mx = 2 αn = 20°
z1 = 1 d1 = 31
γ = 3.691386°
mn = 1.99585
d'p = 3.3363
dp = 3.3
M = 35.3344
2 三量柱跨距 M
表5.25内 公式

（b）斜齿齿轮的计算公式近似代用的方法

这种方法是将斜齿齿轮的量柱( 球) 跨距计算公式做为蜗杆的三量柱跨距计算的代用公式进行跨距计 算。
3 型的蜗杆齿形因为不是渐开线齿形, 所以, 这种方 法只能是一种近似的代用法, 但在实际应用中完全可以满足要求。
表5.26 , 5.27 是轴向模数方式蜗杆的计算表, 表5.28
, 5.29 是法向模数方式蜗杆的计算表。

表5.26 轴向模数方式蜗杆的量柱(球)直径
序号 计算项目 代号 计算方程式 计算例
1 当量齿轮齿数 zv
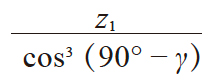
表5.26内 公式
mx = 2
αn = 20°
z1 = 1
d1 = 31
γ = 3.691386°
zv = 3747.1491
ηv = − 0.014485
α'v = 20°
φv = 0.349485
inv φv = 0.014960
d'p = 3.3382
2 齿槽半角 ηv
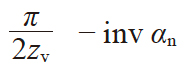
表5.26内 公式
3 量柱与齿面相接点
上的压力角		 α'v
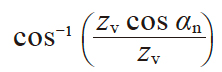
表5.26内 公式
4 通过中心的压力角 φv tan α'v + ηv
5 理想的量柱直径(球) d'p zvmx cos γ cos αn（inv φv + ηv）
注. 角度ηv、φv 的单位为弧度。 表5.27 轴向模数方式蜗杆的三量柱跨距
序号 计算项目 代号 计算方程式 计算例
1 量柱(球)直径 dp 注1 dp = 3.3
αt = 76.96878°
inv αt = 4.257549
inv φ = 4.446297
φ = 80.2959°
M = 35.3345
2 φ 的渐开线函数 inv φ
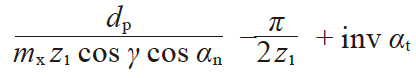
表5.27内 公式
3 通过球心的压力角 φ 由渐开线函数表中查出。
4 三量柱跨距 M
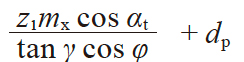
表5.27内 公式
注1. 使用通过表5.26 所求出的量球(柱)直径或与之接近的量柱。 注2. 其中
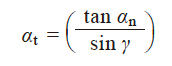
表5.27 注2

下面介绍法向( 齿直角) 模数方式蜗杆的计算方法。
基本上说, 不论是轴向模数还是法向模数方式, 完全可以使用同样的公式进行计算。为了使用做为基准的模数, 将计算公式做了变形。

表5.28 法向模数方式蜗杆量柱(球)的直径
序号 计算项目 代号 计算方程式 计算例
1 当量齿轮齿数 zv
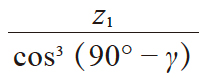
表5.28内 公式
mn = 2.5
αn = 20°
z1 = 1
d1 = 37
γ = 3.874288°
zv = 3241.792
ηv = −0.014420
α'v = 20°
φv = 0.349550
inv φv = 0.0149687
d'p = 4.1785
2 齿槽半角 ηv
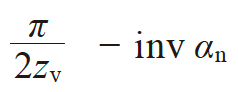
表5.28内 公式
3 量球(柱)与齿面
接点上的压力角		 α'v
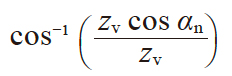
表5.28内 公式
4 通过量球(柱)中心的压力角 φv tan α'v + ηv
5 理想的量球(柱)的直径 d'p zv mn cos αn（inv φv + ηv）
注. 角度ηv、φv 的单位为弧度。 表5.29 法向模数方式蜗杆的三量柱跨距
序号 计算项目 代号 计算方程式 计算例
1 量柱(球)直径 dp 注1 dp = 4.2
αt = 79.48331°
inv αt = 03.999514
inv φ = 04.216536
φ = 79.8947°
M = 42.6897
2 φ 的渐开线函数 inv φ
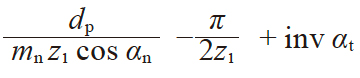
表5.29内 公式
3 通过球心的压力角 φ 由渐开线函数表中查出。
4 三量柱跨距 M
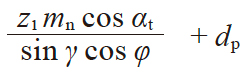
表5.29内 公式
注1. 使用通过表5.28 所求出的量球(柱)直径或与之接近的量柱。 注2. 其中
表5.29 注2
Go to Top