齿轮的大小取决于模数 m 、齿数 z 、压力角 α 、变位系数 x 等齿轮的基本要素。在本章中, 我们将介绍正齿轮、斜齿齿轮、齿条、锥齿轮、交错轴斜齿轮及蜗杆蜗轮等各种齿轮的尺寸计算方法。
这里计算的齿轮外形尺寸(齿顶圆直径等)是齿坯的车削加工时必要的数据, 齿高及齿根圆直径等轮齿尺寸是切齿加工时的参考尺寸。
4.1 正齿轮
齿轮中最为单纯的齿轮是正齿轮。计算也颇为简单,是计算其他齿轮的基础。
下面, 我们将介绍标准正齿轮、变位正齿轮及直线齿形齿条的尺寸计算方法。
标准正齿轮是指变位为零(无变位)的正齿轮。
(1)标准正齿轮
图4.1 示意了标准正齿轮的啮合状况。
图4.1 示意了标准正齿轮的啮合状况。
标准正齿轮的分度圆在相切状态下啮合。
表4.1 为标准正齿轮的计算表。
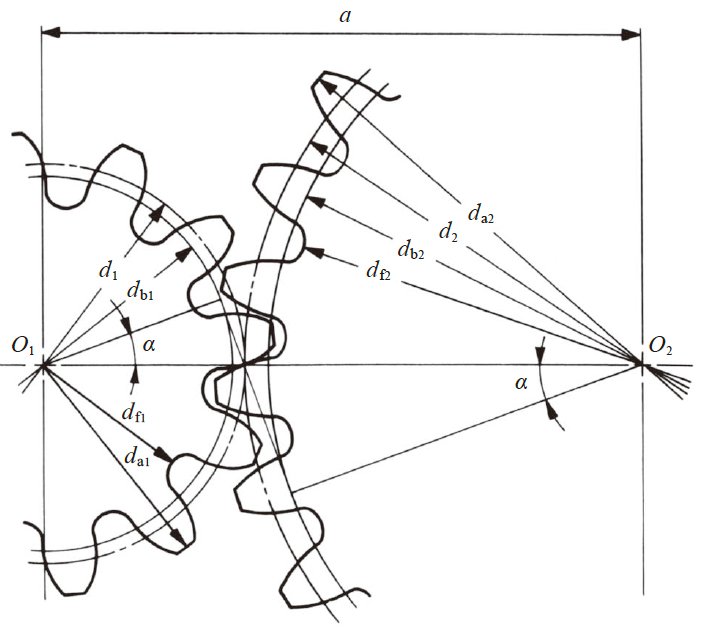
图4.1 标准正齿轮的啮合( α = 20°, z1 = 12, z2 = 24, x1 = x2 = 0 )
表4.1 标准正齿轮的计算表| 序号 | 计算项目 | 代号 | 计算方程式 | 计算例 | |
| 小齿轮(1) | 大齿轮(2) | ||||
| 1 | 模数 | m | 设定值 | 3 | |
| 2 | 分度圆压力角 | α | 20˚ | ||
| 3 | 齿数 | z | 12 | 24 | |
| 4 | 中心距 | a |
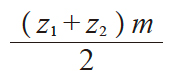
|
54.000 | |
| 5 | 分度圆直径 | d | zm | 36.000 | 72.000 |
| 6 | 基圆直径 | db | d cos α | 33.829 | 67.658 |
| 7 | 齿顶高 | ha | 1.00m | 3.000 | 3.000 |
| 8 | 齿高 | h | 2.25m | 6.750 | 6.750 |
| 9 | 齿顶圆直径 | da | d + 2m | 42.000 | 78.000 |
| 10 | 齿根圆直径 | df | d − 2.5m | 28.500 | 64.500 |
在表4.1 中, 首先指定了模数 m 及齿数 z1 , z2 。与此不同首先决定模数 m 和中心距 a 与传动比 i , 然后计算齿数 z1 , z2 的模式列於表4.2。
表4.2 齿数的求法| 序号 | 计算项目 | 代号 | 计算方程式 | 计算例 | ||
| 小齿轮(1) | 大齿轮(2) | |||||
| 1 | 模数 | m | 设定值 | 3 | ||
| 2 | 中心距 | α | 54.000 | |||
| 3 | 传动比 | i | 1.25 | |||
| 4 | 齿数的和 | z1 + z2 | 2a / m | 36 | ||
| 5 | 齿数 | z |
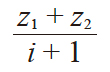
|
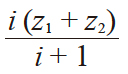
|
16 | 20 |
如上例所示, 齿数刚好成为整数。但是, 在实际计算时并非如此. 象这种情况下, 对齿轮实行变位或者用斜齿齿轮代替正齿轮的话, 可以得到与所需的传动比相近的数值。
(2)变位正齿轮
图4.2 为变位齿轮的啮合示意图。
变位正齿轮的啮合最重要的是啮合节圆直径 dw 和压力角 αw 。
这些数值, 可依据变位正齿轮的中心距 a 利用下列方程式求出。
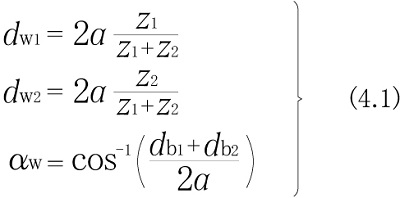
变位齿轮与这个啮合圆相切啮合。啮合节圆的压力角即为啮合压力角。
表4.3 中, 示意了首先确定变位系数 x1 , x2 后计算齿轮参数的方法。这个变位计算是以保持顶隙 c 为0.25m的设定为基础。
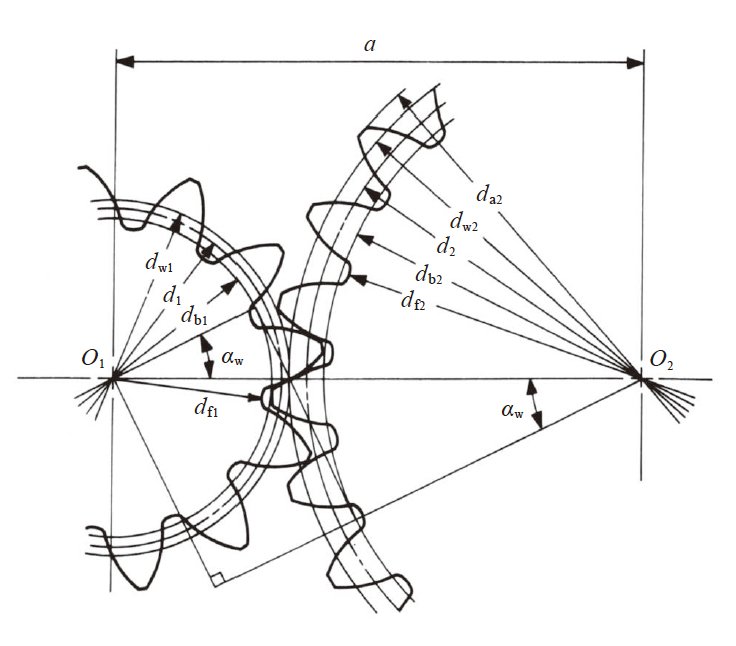
图4.2 变位齿轮的啮合( α = 20°, z1 = 12, z2= 24, x1 = + 0.6, x2 = + 0.36 )
表4.3 变位正齿轮的计算(1)| 序号 | 计算项目 | 代号 | 计算方程式 | 计算例 | |
| 小齿轮(1) | 大齿轮(2) | ||||
| 1 | 模数 | m | 设定值 | 3 | |
| 2 | 压力角 | α | 20˚ | ||
| 3 | 齿数 | z | 12 | 24 | |
| 4 | 变位系数 | x | 0.6 | 0.36 | |
| 5 | αw角的渐开线函数 | inv αw |
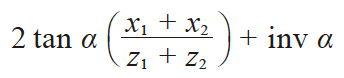
|
0.034316 | |
| 6 | 啮合压力角 | αw | 由渐开线函数表中求出 | 26.0886˚ | |
| 7 | 中心距变动系数 | y |
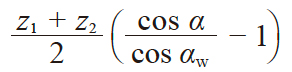
|
0.83329 | |
| 8 | 中心距 | a |
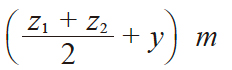
|
56.4999 | |
| 9 | 分度圆直径 | d | zm | 36.000 | 72.000 |
| 10 | 基圆直径 | db | d cos α | 33.8289 | 67.6579 |
| 11 | 啮合节径 | dw | db / cos αw | 37.667 | 75.333 |
| 12 | 齿顶高 | ha1 ha2 |
( 1 + y − x2 )m ( 1 + y − x1 )m |
4.420 | 3.700 |
| 13 | 全齿高 | h | { 2.25 + y − ( x1 + x2 )}m | 6.370 | |
| 14 | 齿顶圆直径 | da | d + 2ha | 44.840 | 79.400 |
| 15 | 齿根圆直径 | df | da − 2h | 32.100 | 66.660 |
变位齿轮的计算中, 当 x1 = x2 = 0 时, 即为标准齿轮的计算。
计算表(1) 中的第4 到第8 项的顺序颠倒以后进行计算时, 如方法(2)。
表4.4 变位齿轮的计算(2)| 序号 | 计算项目 | 代号 | 计算方程式 | 计算例 | |
| 小齿轮(1) | 大齿轮(2) | ||||
| 1 | 中心距 | a | 设定值 | 56.4999 | |
| 2 | 中心距变动系数 | y |
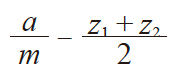
|
0.8333 | |
| 3 | 啮合压力角 | αw |
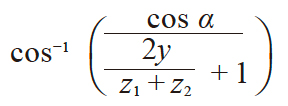
|
26.0886˚ | |
| 4 | 变位系数和 | x1 + x2 |
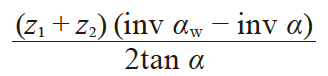
|
0.9600 | |
| 5 | 变位系数 | x | ― | 0.6000 | 0.3600 |
变位系数的和 x1 + x2 采用什么方法分配到每个齿轮上, 有着各种各样的提案。例如, 比较著名的有BSS(英国国家规格), DIN(德国国家规格)等。在这里, 我们将省略对此问题的说明。
在这个例子中, 即防止根切, 又不使齿顶变尖地为小齿轮(z1 = 12) 选择了变位系数。
(3)齿条和正齿轮
在这里, 我们将介绍齿条与正齿轮的啮合及计算方法。
在图4.3(1) 中, 我们已经示意了标准正齿轮与齿条的啮合状况。这个啮合中, 标准正齿轮的分度圆与齿条的节线相切。
图4.3(2) 示意了变位正齿轮和齿条的啮合状态。变位正齿轮的分度圆和齿条的节线离开变位量xm 的距离啮合。
表4.5 中, 示意了齿条和变位正齿轮啮合的计算方法。当表中的变位系数 x1 = 0 时, 可以做为无变位标准正齿轮的计算公式加以使用。
| 序号 | 计算项目 | 代号 | 计算方程式 | 计算例 | |
| 正齿轮 | 齿条 | ||||
| 1 | 模数 | m | 设定值 | 3 | |
| 2 | 压力角 | α | 20˚ | ||
| 3 | 齿数 | z | 12 | — | |
| 4 | 变位系数 | x | 0.6 | ||
| 5 | 节线高度 | H | — | 32.000 | |
| 6 | 啮合压力角 | αw | 20° | ||
| 7 | 装配距离 | a | 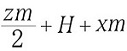 |
51.800 | |
| 8 | 分度圆直径 | d | zm | 36.000 | — |
| 9 | 基圆直径 | db | d cos α | 33.829 | |
| 10 | 啮合节径 | dw | db / cos αw | 36.000 | |
| 11 | 齿顶高 | ha | m ( 1 + x ) | 4.800 | 3.000 |
| 12 | 全齿高 | h | 2.25m | 6.750 | |
| 13 | 齿顶圆直径 | da | d + 2ha | 45.600 | — |
| 14 | 齿根圆直径 | df | da − 2h | 32.100 | |
齿条与正齿轮啮合时, 正齿轮旋转一周时的齿条移动量l 为分度圆齿距的齿数倍。
l = πmz(4.2)
齿条的移动量l 不受齿轮变位的影响, 只由齿条的分度圆齿距πm 和正齿轮的齿数z 来决定。
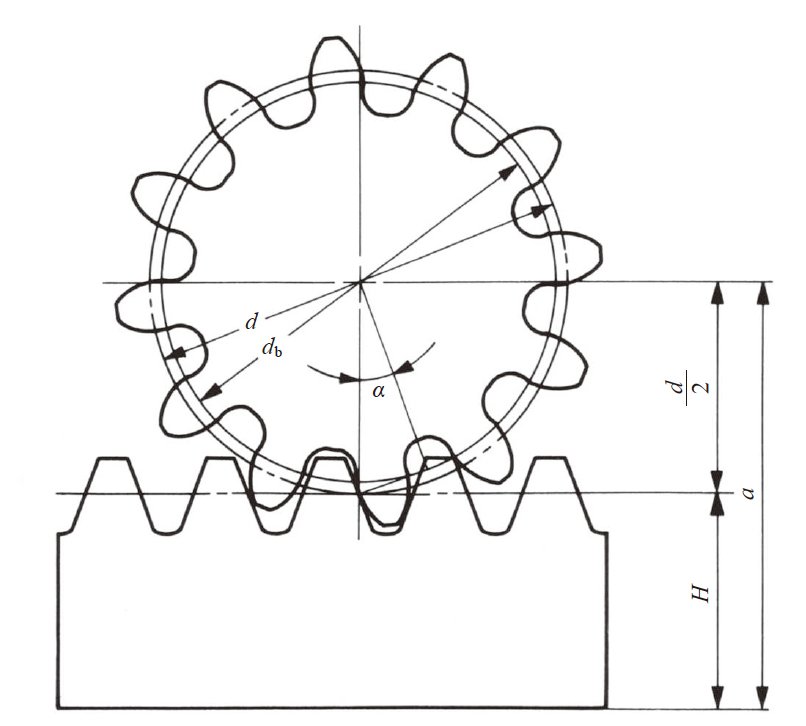
图4.3(1) 标准正齿轮与齿条的啮合( α = 20°, z1 = 12, x1 = 0 )
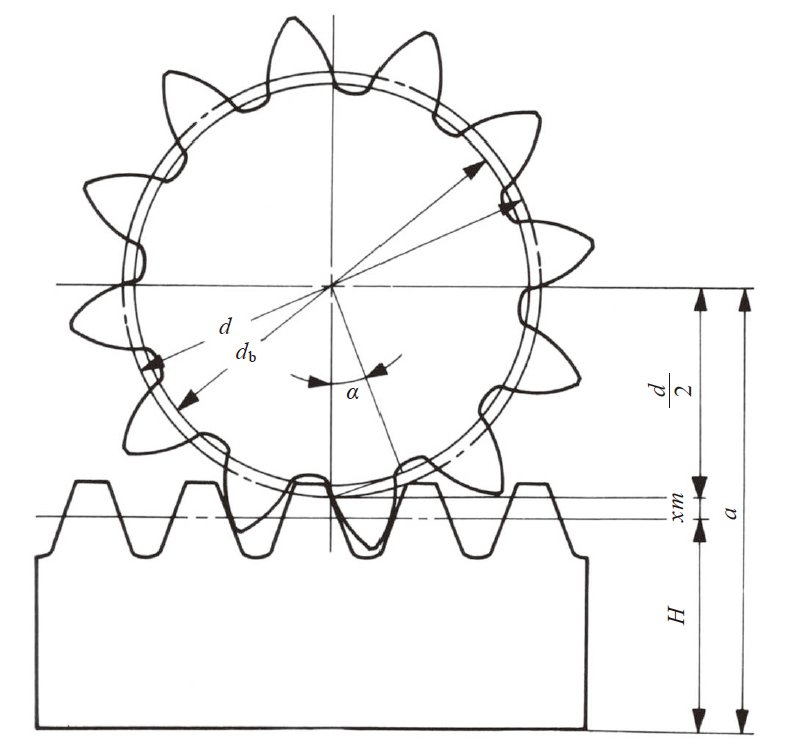
图4.3(2) 变位正齿轮与齿条的啮合( α = 20°, z1 = 12, x1 = + 0.6 )
4.2 内齿轮
内齿轮是在圆筒的内侧加工有轮齿, 与正齿轮啮合使用的齿轮。内齿轮的轮齿是正齿轮的齿槽部分的齿形。
内齿轮的齿形是凹齿形, 与正齿轮的齿形相反。下面我们就变位内齿轮的尺寸计算方法及内齿轮的干涉问题做以介绍。
(1)变位内齿轮的计算
图4.4 中示意了内齿轮与正齿轮的啮合状况。
内齿轮和外齿轮啮合时, 最重要的是啮合节径 dw 和啮合压力角 αw 。
具体的数据可以根据变位齿轮的中心距 a 利用下式简单地求出。
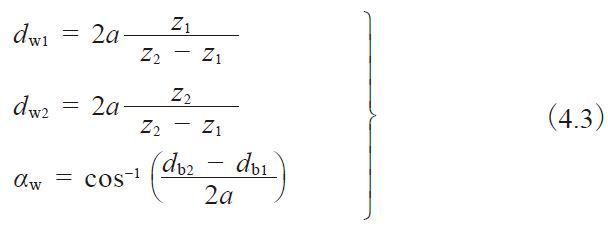
表4.6 中, 列出了变位内齿轮与正齿轮的计算方法。
计算标准齿轮时, 我们推荐将式中的 x1 = x2 = 0 进
行计算。
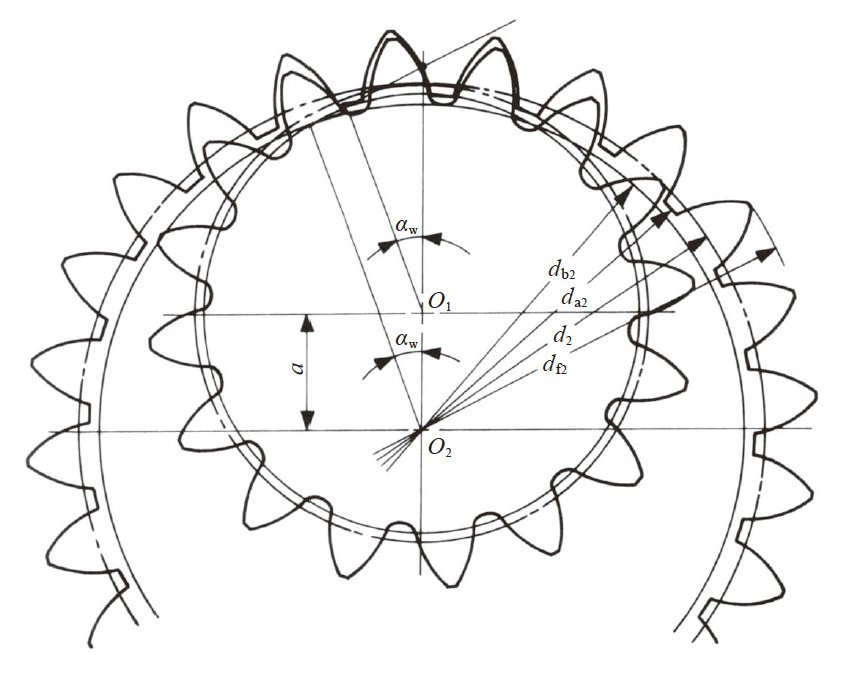
图4.4 内齿轮与正齿轮的啮合( α = 20°, z1 = 16, z2= 24, x1 = x2 = + 0.5 )
表4.6 变位内齿轮和正齿轮的计算(1)| 序号 | 计算项目 | 代号 | 计算方程式 | 计算例 | |
| 正齿轮(1) | 内齿轮(2) | ||||
| 1 | 模数 | m | 设定值 | 3 | |
| 2 | 压力角 | α | 20˚ | ||
| 3 | 齿数 | z | 16 | 24 | |
| 4 | 变位系数 | x | 0 | + 0.516 | |
| 5 | 渐开线函数 | inv αw |
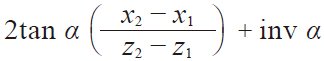
|
0.061857 | |
| 6 | 啮合压力角 | αw | 由渐开线函数表中求出 | 31.321258° | |
| 7 | 中心距变动系数 | y | 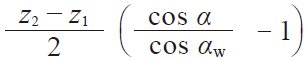 |
0.4000 | |
| 8 | 中心距 | a | 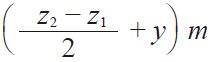 |
13.2 | |
| 9 | 分度圆直径 | d | zm | 48.000 | 72.000 |
| 10 | 基圆直径 | db | d cos α | 45.105 | 67.658 |
| 11 | 啮合节径 | dw | db / cos αw | 52.7998 | 79.1997 |
| 12 | 齿顶高 | ha1 ha2 |
( 1 + x1 ) m ( 1 − x2 ) m |
3.000 | 1.452 |
| 13 | 全齿高 | h | 2.25m | 6.75 | |
| 14 | 齿顶圆直径 | da1 da2 |
d1 + 2ha1 d2 − 2ha2 |
54.000 | 69.096 |
| 15 | 齿根圆直径 | df1 df2 |
da1 − 2h da2 + 2h |
40.500 | 82.596 |
做为齿轮的要素, 如果首先在中心距 a 一定的情况下求得变位系数 x1 , x2 时, 将表4.6 中的第4 到第8 的
五个计算项目的顺序颠倒过来进行计算 , 计算方法列于表 4.7。
| 序号 | 计算项目 | 代号 | 计算方程式 | 计算例 | |
| 正齿轮(1) | 内齿轮(2) | ||||
| 1 | 中心距 | a | 设定值 | 13.1683 | |
| 2 | 中心距变动系数 | y | 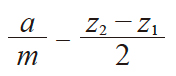 |
0.38943 | |
| 3 | 啮合压力角 | αw | 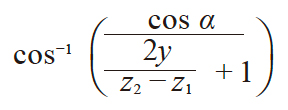 |
31.0937° | |
| 4 | 变位系数的差 | x2 − x1 | 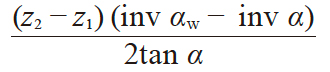 |
0.5 | |
| 5 | 变位系数 | x | ― | 0 | 0.5 |
内齿轮或正齿轮在使用小齿轮铣刀切齿时, 加工齿轮的齿高及齿根圆直径可能与根据上式所计算的数据不同。这是因为受到齿数及小齿轮铣刀变位的影响. 要想得到正确的尺寸, 需要根据小齿轮铣刀的变位系数进行计算。
(2)内齿轮的干涉
内齿轮与外齿轮在啮合时, 容易发生渐开曲线干涉、次摆线干涉、齿轮间干涉等具有代表性的三种干涉。
(a)渐开曲线干涉
渐开曲线干涉是正齿轮的齿根与内齿轮的齿顶间的干涉, 容易发生在正齿轮的齿数较少时。
避免渐开曲线干涉发生的条件是:

其中 αa2:内齿轮的齿顶压力角

αw:啮合压力角
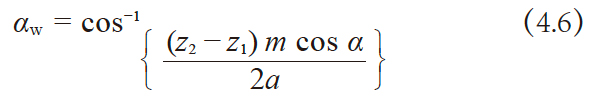
要想使(4.5) 公式成立的必要条件是内齿轮的齿顶圆大于基圆。
da2 ≧ db2(4.7)
分度圆压力角 α = 20°的标准齿轮, 如果齿数不满足条件 z2 > 34 的话, 内齿轮的齿顶圆无法比基圆大。
(b)次摆线干涉
次摆线干涉是正齿轮的齿顶离开齿槽时, 与内齿轮的齿顶间产生干涉, 容易发生在内齿轮与正齿轮的齿数差较小时。
不产生次摆线干涉的条件由公式(4.8) 求出。计算时,式中应力角(α) 等角度单位请使用弧度。
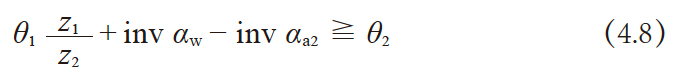
其中
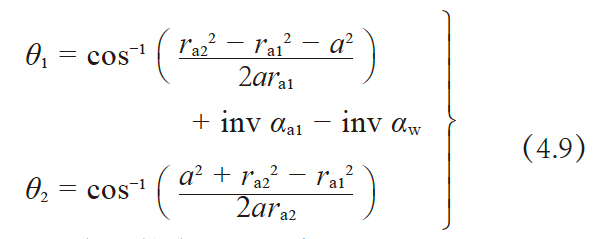
其中 αa1 是正齿轮的齿顶压力角

通过计算可以得出, 分度圆压力角 α = 20° 的标准内齿轮与标准正齿轮啮合时齿数差 z2 - z1 只要大于9,就不会发生次摆线干涉。
(c)径向干涉
径向干涉是指正常啮合的内齿轮与正齿轮间, 正齿轮无法从啮合位置沿半径方向移动的干涉, 容易发生在内齿轮与正齿轮的齿数差小时。
不发生此干涉的条件如式(4.11) 所示。
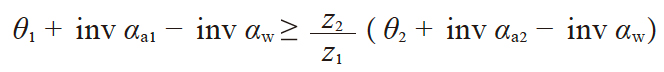
其中
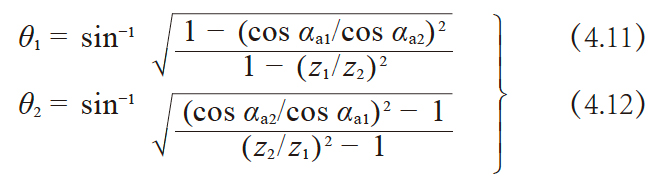
即使发生此干涉, 只要将齿轮沿轴方向移动并使之啮合后, 对通常齿轮的啮合完全不产生任何影响。
但是, 当使用小齿轮铣刀展成内齿轮时, 这种干涉就成了重大的问题。也就是说, 发生干涉时, 小齿轮铣刀从内齿轮脱出时, 由于干涉的影响刀具有发生破损的可能。
刀具压力角 α0=20°的标准内齿轮利用无变位的(x0 = 0)小齿轮铣刀进行切齿时, 不发生径向干涉的内齿轮齿数极限值列于表4.8(1)。
| z0 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 24 | 25 | 27 |
| z2 | 34 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 42 | 43 | 43 |
| z0 | 28 | 30 | 31 | 32 | 33 | 34 | 35 | 38 | 40 | 42 |
| z2 | 46 | 48 | 49 | 50 | 51 | 52 | 53 | 56 | 58 | 60 |
| z0 | 44 | 48 | 50 | 56 | 60 | 64 | 66 | 80 | 96 | 100 |
| z2 | 62 | 66 | 68 | 74 | 78 | 82 | 84 | 98 | 114 | 118 |
此表中, z0 = 15 ~ 22 时, 将发生渐开曲线干涉。
( z0 为小齿轮铣刀的齿数)
表4.8(2) 列出了利用变位小齿轮铣刀切削标准内齿轮时, 不发生径向干涉的内齿轮的齿数。
此时, 设 x0 = 0.0075z0 + 0.05。
| z0 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 24 | 25 | 27 |
| x0 | 0.1625 | 0.17 | 0.1775 | 0.185 | 0.1925 | 0.2 | 0.2075 | 0.215 | 0.23 | 0.2375 | 0.2525 |
| z2 | 36 | 38 | 39 | 40 | 41 | 42 | 43 | 45 | 47 | 48 | 50 |
| z0 | 28 | 30 | 31 | 32 | 33 | 34 | 35 | 38 | 40 | 42 |
| x0 | 0.26 | 0.275 | 0.2825 | 0.29 | 0.2975 | 0.305 | 0.3125 | 0.335 | 0.35 | 0.365 | z2 | 52 | 54 | 55 | 56 | 58 | 59 | 60 | 64 | 66 | 68 |
| z0 | 44 | 48 | 50 | 56 | 60 | 64 | 66 | 80 | 96 | 100 |
| x0 | 0.38 | 0.41 | 0.425 | 0.47 | 0.5 | 0.53 | 0.545 | 0.65 | 0.77 | 0.8 | z2 | 71 | 76 | 78 | 86 | 90 | 95 | 98 | 115 | 136 | 141 |
此表中, 当z0 = 15 ~ 19 时, 将发生渐开曲线干涉,内齿轮齿顶的一部分正确的渐开线齿形会被切削掉。
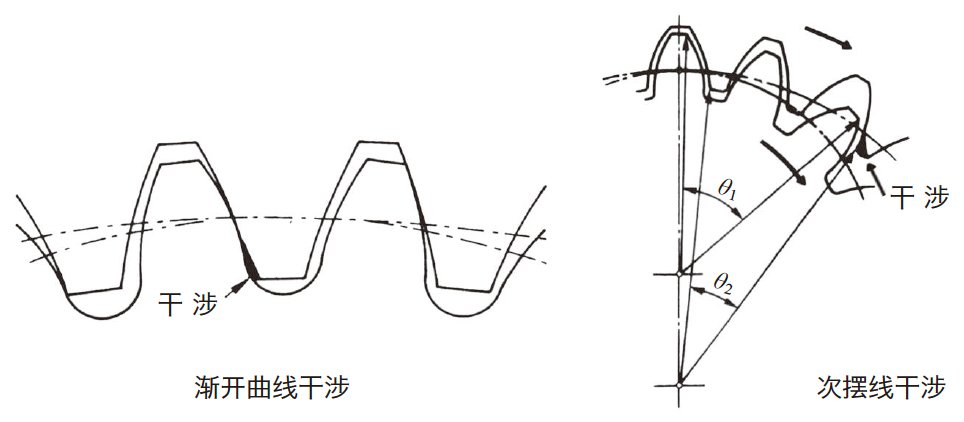
图4.5 渐开曲线干涉和次摆线干涉
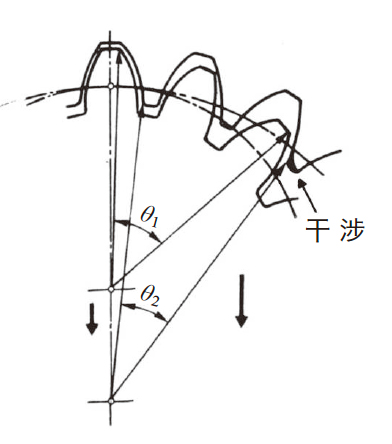
图4.6 径向干涉
4.3 斜齿齿轮
如图4.7 所示, 斜齿齿轮是齿线呈螺旋线的圆柱齿轮。在分度圆上, 螺旋线拥有螺旋角 β, 旋转一周的进程为 pz 。
斜齿齿轮的齿形曲线, 从正面看为渐开线曲线, 齿形有齿直角方式与轴直角方式二种。
沿齿直角螺旋线测定的齿距 pn(法向齿距)除以圆周率 π 的数值为法向模数 mn 。
mn = pn / π(4.13)
以法向模数 mn 和法向压力角 αn 为基准的齿轮为齿直角方式斜齿齿轮。
与同时垂直于轴平面和节面的平面( 即端面) 上测定的分度圆柱上的齿距 pt(端面齿距)除以圆周率 π 的数值为端面模数 mt 。
mt = pt / π(4.14)
以端面模数 mt 和端面压力角 αt 为基准的齿轮为轴直角方式斜齿齿轮。
齿直角方式斜齿齿轮的模数 mn 和压力角 αn 只要相同, 分度圆螺旋角 β 即使不同也可以利用相同的滚刀进行切齿加工。
但是, 虽然轴直角方式斜齿齿轮的模数 mt 和压力角 αt 相同, 分度圆螺旋角 β 不同的话, 切齿时就必须更换滚刀。
因为制作容易, 齿直角方式斜齿齿轮非常普及。
在平行轴使用斜齿齿轮啮合时, 必须使用螺旋角相同, 螺旋方向相反的齿轮副。
螺旋角不同的斜齿齿轮, 不能在平行轴上啮合, 只能在交错轴上啮合, 所以, 称为交错轴斜齿轮。
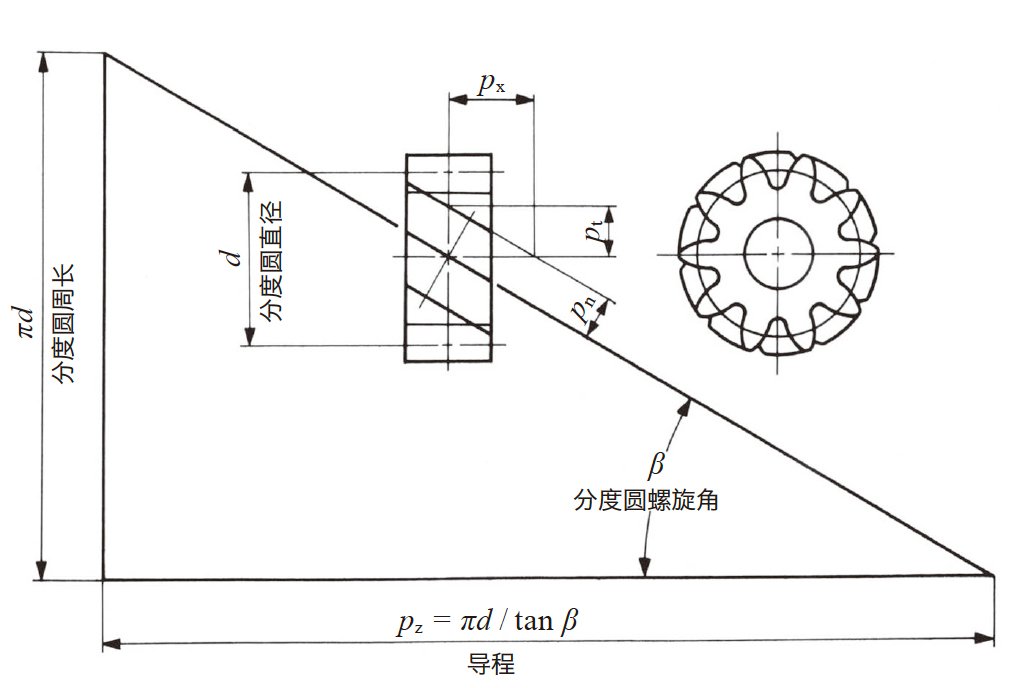
图4.7 斜齿齿轮(右旋齿)
(1)齿直角方式斜齿齿轮
啮合节径 dw 和端面压力角 αwt 对于变位斜齿齿轮的啮合而言亦是重要的要素。从端面来考虑的话, 正齿轮和斜齿齿轮的啮合是相同的, 所以计算方程式也相同。
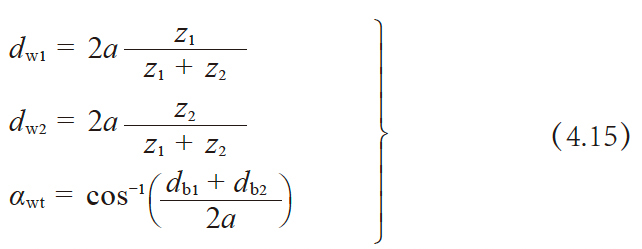
表4.9 是齿直角方式变位斜齿齿轮的计算表。计算标准斜齿齿轮时, 式中的 xn1 = xn2 = 0 。
表4.9 齿直角方式变位斜齿齿轮的计算(1)| 序号 | 计算项目 | 代号 | 计算方程式 | 计算例 | |
| 小齿轮(1) | 大齿轮(2) | ||||
| 1 | 法向模数 | mn | 设定值 | 3 | |
| 2 | 法向压力角 | αn | 20° | ||
| 3 | 分度圆螺旋角 | β | 30° | ||
| 4 | 齿数(螺旋方向) | z | 12(L) | 60(R) | |
| 5 | 法向变位系数 | xn | + 0.09809 | 0 | |
| 6 | 端面压力角 | αt |
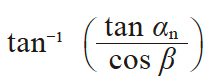
|
22.79588° | |
| 7 | 渐开线函数 αwt | inv αwt |
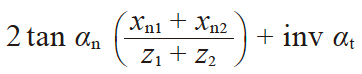
|
0.023405 | |
| 8 | 端面啮合压力角 | αwt | 由渐开线函数表中查出 | 23.1126° | |
| 9 | 中心距变动系数 | y |
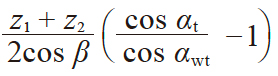
|
0.09744 | |
| 10 | 中心距 | a |
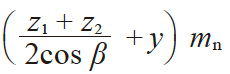
|
125.000 | |
| 11 | 分度圆直径 | d | zmn / cos β | 41.569 | 207.846 |
| 12 | 基圆直径 | db | d cos αt | 38.322 | 191.611 |
| 13 | 啮合节径 | dw | db / cos αwt | 41.667 | 208.333 |
| 14 | 齿顶高 | ha1 ha2 |
( 1 + y − xn2 )mn ( 1 + y − xn1 )mn |
3.292 | 2.998 |
| 15 | 全齿高 | h | { 2.25 + y −( xn1 + xn2 )}mn | 6.748 | |
| 16 | 齿顶圆直径 | da | d + 2ha | 48.153 | 213.842 |
| 17 | 齿根圆直径 | df | da − 2h | 34.657 | 200.346 |
当齿轮的中心距 a 一定的条件下求变位系数 xn1 , xn2时, 将表4.9 中的第5 到第10 项按相反的顺序进行计算。
计算结果列于表4.10。
| 序号 | 计算项目 | 代号 | 计算方程式 | 计算例 | |
| 小齿轮(1) | 大齿轮(2) | ||||
| 1 | 中心距 | a | 设定值 | 125 | |
| 2 | 中心距变动系数 | y |
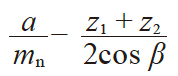
|
0.097447 | |
| 3 | 端面啮合压力角 | αwt |
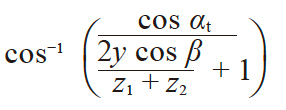
|
23.1126° | |
| 4 | 变位系数的和 | xn1 + xn2 |
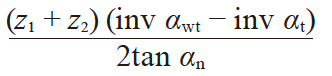
|
0.09809 | |
| 5 | 齿直角变位系数 | xn | ― | 0.09809 | 0 |
齿直角方式斜齿齿轮与轴直角方式斜齿齿轮的换算关系如下:
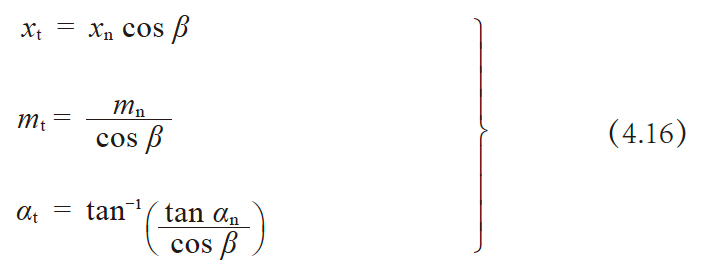
(2)轴直角方式斜齿齿轮
表4.11 是轴直角方式变位斜齿齿轮的计算表。计算标准斜齿齿轮时, 取 xt1 = xt2 = 0 。
表4.11 轴直角方式变位斜齿齿轮的计算(1)| 序号 | 计算项目 | 代号 | 计算方程式 | 计算例 | |
| 小齿轮(1) | 大齿轮(2) | ||||
| 1 | 端面模数 | mt | 设定值 | 3 | |
| 2 | 端面压力角 | αt | 20° | ||
| 3 | 分度圆螺旋角 | β | 30° | ||
| 4 | 齿数(螺旋方向) | z | 12(L) | 60(R) | |
| 5 | 切向变位系数 | xt | 0.34462 | 0 | |
| 6 | 渐开线函数αwt | inv αwt |
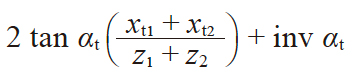
|
0.0183886 | |
| 7 | 端面啮合压力角 | αwt | 由渐开线函数表中查出 | 21.3975° | |
| 8 | 中心距变动系数 | y |
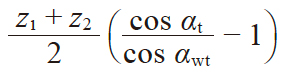
|
0.33333 | |
| 9 | 中心距 | a |
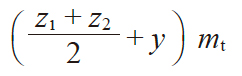
|
109.0000 | |
| 10 | 分度圆直径 | d | zmt | 36.000 | 180.000 |
| 11 | 基圆直径 | db | d cos αt | 33.8289 | 169.1447 |
| 12 | 啮合节径 | dw | db / cos αwt | 36.3333 | 181.6667 |
| 13 | 齿顶高 | ha1 ha2 |
( 1 + y − xt2 )mt ( 1 + y − xt1 )mt |
4.000 | 2.966 |
| 14 | 全齿高 | h | { 2.25 + y −( xt1 + xt2 )}mt | 6.716 | |
| 15 | 齿顶圆直径 | da | d + 2ha | 44.000 | 185.932 |
| 16 | 齿根圆直径 | df | da − 2h | 30.568 | 172.500 |
表(2) 是按相反顺序计算表4.11 的第5 项到第9 项的结果。
表4.12 轴直角方式变位斜齿齿轮的计算(2)| 序号 | 计算项目 | 代号 | 计算方程式 | 计算例 | |
| 小齿轮(1) | 大齿轮(2) | ||||
| 1 | 中心距 | a | 设定值 | 109 | |
| 2 | 中心距变动系数 | y |
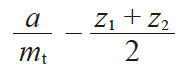
|
0.33333 | |
| 3 | 端面啮合压力角 | αwt |
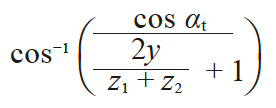
|
21.39752° | |
| 4 | 变位系数的和 | xt1 + xt2 |
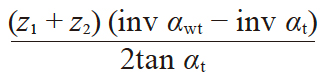
|
0.34462 | |
| 5 | 切向变位系数 | xt | ― | 0.34462 | 0 |
轴直角方式斜齿齿轮与齿直角方式斜齿齿轮的换算关系如下:
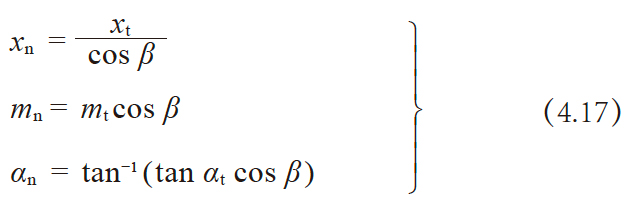
(3)斜齿齿条
斜齿轮与斜齿条的啮合从正面(轴直角方向)看上去,与齿条和正齿轮的啮合完全相同。
表4.13 为齿直角方式斜齿条的计算, 表4.14 为轴直角方式斜齿条的计算。
| 序号 | 计算项目 | 代号 | 计算方程式 | 计算例 | |
| 斜齿齿轮 | 斜齿齿条 | ||||
| 1 | 法向模数 | mn | 设定值 | 2.5 | |
| 2 | 法向压力角 | αn | 20° | ||
| 3 | 分度圆螺旋角 | β | 10°57′49″ | ||
| 4 | 齿数(螺旋方向) | z | 20(R) | ─(L) | |
| 5 | 法向变位系数 | xn | 0 | ─ | |
| 6 | 节线高度 | H | ─ | 27.5 | |
| 7 | 端面压力角 | αt |
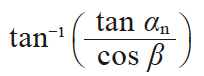
|
20.34160° | |
| 8 | 装配距离 | a |
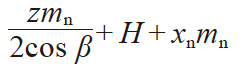
|
52.965 | |
| 9 | 分度圆直径 | d | zmn / cos β | 50.92956 | ─ |
| 10 | 基圆直径 | db | d cos αt | 47.75343 | |
| 11 | 齿顶高 | ha | mn( 1 + xn ) | 2.500 | 2.500 |
| 12 | 全齿高 | h | 2.25mn | 5.625 | |
| 13 | 齿顶圆直径 | da | d + 2ha | 55.929 | ─ |
| 14 | 齿根圆直径 | df | da − 2h | 44.679 | |
当表中 xn = 0 时, 即为无变位齿直角齿轮的计算。
齿直角方式斜齿齿条与斜齿齿轮在平行轴相互啮合时, 螺旋角相等, 旋向相反是必要条件。
斜齿齿轮旋转一周时齿条的位移量 l 齿条端面齿距的齿数倍。

表4.13 的情况下, 端面齿距 pt 为8mm, 所以位移l为160 mm。
如上所述, 只要适当地选择螺旋角, 端面齿距 pt 可以成为整数。
| 序号 | 计算项目 | 代号 | 计算方程式 | 计算例 | |
| 斜齿齿轮 | 斜齿齿条 | ||||
| 1 | 端面模数 | mt | 设定值 | 2.5 | |
| 2 | 端面压力角 | αt | 20° | ||
| 3 | 螺旋角 | β | 10°57′49″ | ||
| 4 | 齿数(螺旋方向) | z | 20(R) | ─(L) | |
| 5 | 切向变位系数 | xt | 0 | ─ | |
| 6 | 节线高度 | H | ─ | 27.5 | |
| 7 | 装配距离 | a |
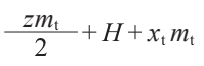
|
52.500 | |
| 8 | 分度圆直径 | d | zmt | 50.000 | ─ |
| 9 | 基圆直径 | db | d cos αt | 46.98463 | |
| 10 | 齿顶高 | ha | mt( 1 + xt ) | 2.500 | 2.500 |
| 11 | 全齿高 | h | 2.25mt | 5.625 | |
| 12 | 齿顶圆直径 | da | d + 2ha | 55.000 | ─ |
| 13 | 齿根圆直径 | df | da − 2h | 43.750 | |
轴直角方式斜齿齿条和斜齿轮啮合时, 斜齿轮旋转一周时齿条的位移量l 是齿条的端面齿距的齿数倍。
l = πmt z(4.19)
4.4 锥齿轮
锥齿轮是在相交的两轴之间做传动的圆锥齿轮。根据齿线的形状, 分为直齿锥齿轮、弧齿锥齿轮、零度齿锥齿轮。锥齿轮是拥有锥形节圆面的两个齿轮在即相切又不产生滑动的状态下做啮合传动的齿轮。
齿数为z1 的小齿轮和齿数为 z2 的大齿轮在轴交角为 Σ ( 相交两轴间的夹角) 啮合时, 各自的分度圆锥角 δ1、δ2 的计算方法如下所示。
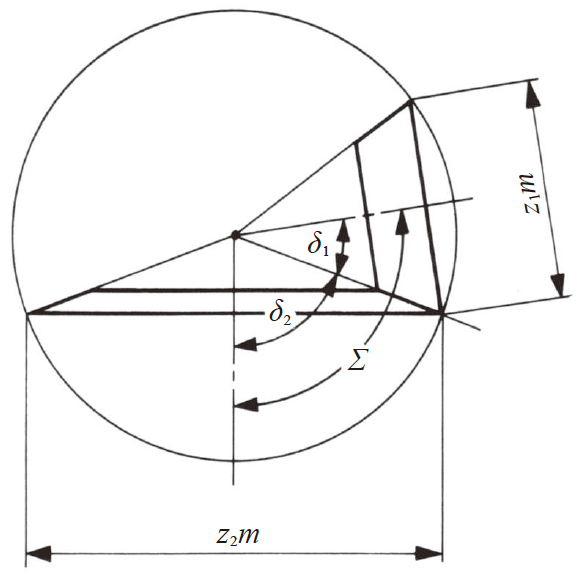
图4.8 锥齿轮的分度圆锥角
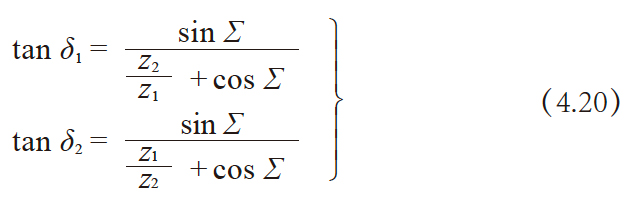
轴交角Σ 为直角的情形最为常见。除直角外, 也在锐角及钝角的状态下使用。在锐角及钝角的状态下使用的锥齿轮被称为斜交锥齿轮。图4.8 示意了钝角锥齿轮的情形。
轴交角 Σ = 90°时, 方程式(4.20) 变化如下。

轴交角Σ = 90°, 齿数比 z2 / z1 = 1 的锥齿轮被称为等径锥齿轮。
图4.9 示意了锥齿轮的啮合。
锥齿轮的啮合必须在齿轮副的情况下加以考虑。被决定的齿数以外的组合无法正确地啮合。
锥齿轮的啮合, 如果如图4.9 所示, 由端面做基准去考虑的话, 可以得到与正齿轮的啮合很近似的结果。
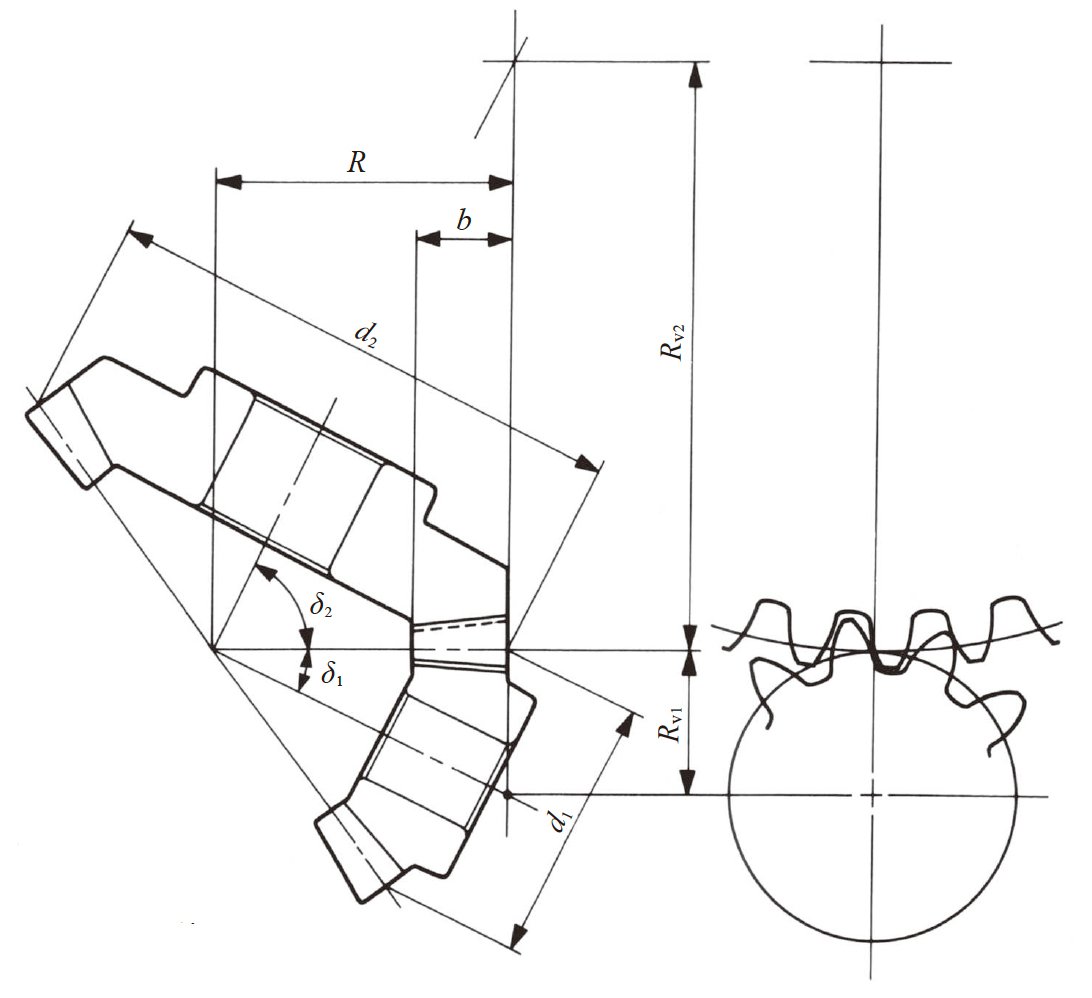
图4.9 锥齿轮的啮合
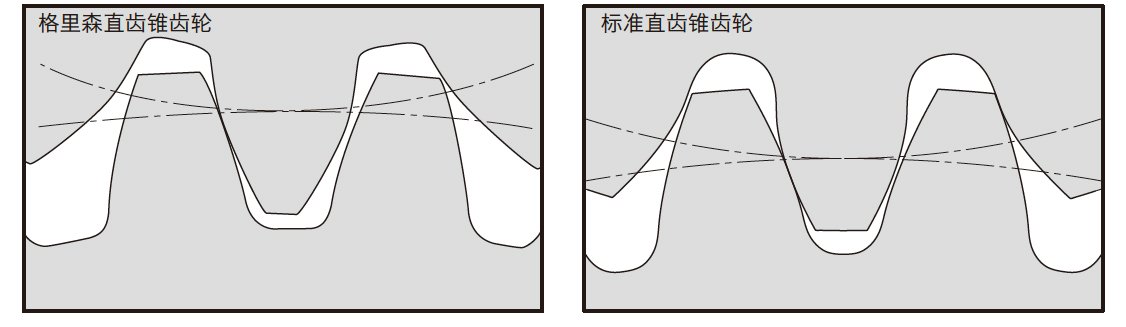
(1)格里森直齿锥齿轮
直齿锥齿轮是齿线为沿圆锥面指向圆锥顶点的直线锥齿轮。
直齿锥齿轮有格里森直齿锥齿轮和标准直齿锥齿轮两种具有代表性的方式。
这里介绍的格里森直齿锥齿轮的齿形为齿高 h = 2.188m, 顶隙 c = 0.188m, 工作齿高 hw = 2.000m。
这种齿轮的特点是:
- ○ 变位齿轮。
- 通过对小齿轮正变位, 大齿轮负变位处理, 使强度平衡得以保证。
但是, 大小齿轮齿数相等的等径齿轮不进行变位。 - ○ 平行顶隙。
- 齿顶圆锥母线和配对齿轮的齿底圆锥母线平行。
轴交角 Σ = 90°的格里森直齿锥齿轮的防止产生根切的最小齿数列于表4.15。
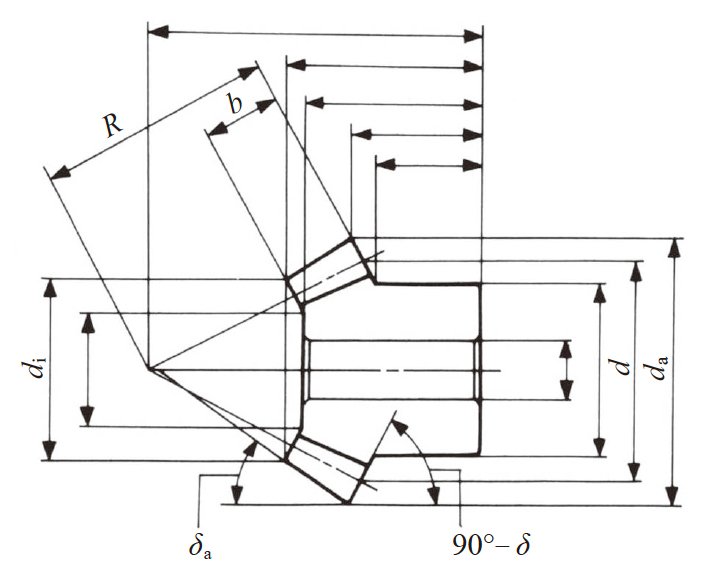
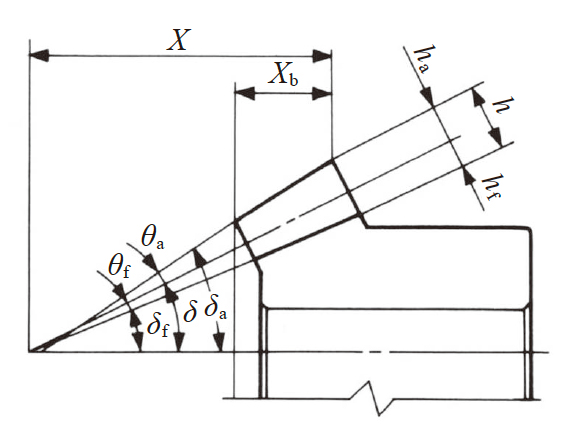
图4.10 锥齿轮的尺寸及角度
表4.15 防止根切的最小齿数| 分度圆压力角 | 齿数的组合 z1 / z2 | |||||
| (14.5°) | 29/29 以上 | 28/29 以上 | 27/31 以上 | 26/35 以上 | 25/40 以上 | 24/57 以上 |
| 20° | 16/16 以上 | 15/17 以上 | 14/20 以上 | 13/30 以上 | ||
| (25°) | 13/13 以上 | |||||
表4.16 是格里森直齿锥齿轮的计算表。计算出的尺寸及角度示意于图4.10。
表4.16 也可计算斜交直齿锥齿轮。
在格里森公司, 将经过鼓形加工的直齿锥齿轮称为弯曲圆锥磨削齿轮(coniflex)。经过此加工的齿轮对防止由于组装误差而引起的片面接触非常有效。
| 序号 | 计算项目 | 代号 | 计算方程式 | 计算例 | |
| 小齿轮(1) | 大齿轮(2) | ||||
| 1 | 轴交角 | Σ | 设定值 | 90° | |
| 2 | 大端模数 | m | 3 | ||
| 3 | 分度圆压力角 | α | 20° | ||
| 4 | 齿数 | z | 20 | 40 | |
| 5 | 分度圆直径 | d | zm | 60 | 120 |
| 6 | 分锥角 |
δ1 δ2 |
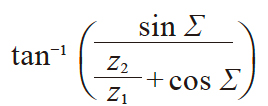
Σ − δ1 |
26.56505° | 63.43495° |
| 7 | 大端锥距 | R |
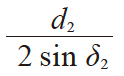
|
67.08204 | |
| 8 | 齿宽 | b | 最好能控制在 R / 3 或10 m 以下 | 22 | |
| 9 | 大端齿顶高 | ha1 ha2 |
2.000m − ha2
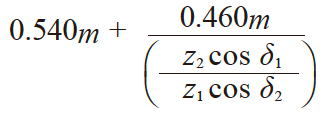
|
4.035 | 1.965 |
| 10 | 大端齿根高 | hf | 2.188m − ha | 2.529 | 4.599 |
| 11 | 齿根角 | θf | tan−1 ( hf / R ) | 2.15903° | 3.92194° |
| 12 | 齿顶角 | θa1 θa2 |
θf2 θf1 |
3.92194° | 2.15903° |
| 13 | 顶锥角 | δa | δ + θa | 30.48699° | 65.59398° |
| 14 | 根锥角 | δf | δ − θf | 24.40602° | 59.51301° |
| 15 | 大端齿顶圆直径 | da | d + 2ha cos δ | 67.2180 | 121.7575 |
| 16 | 冠顶距 | X | R cos δ − ha sin δ | 58.1955 | 28.2425 |
| 17 | 齿顶间轴向距 | Xb |
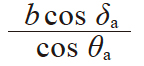
|
19.0029 | 9.0969 |
| 18 | 小端齿顶圆直径 | di |
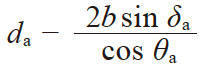
|
44.8425 | 81.6609 |
格里森直齿锥齿轮的特点是变位。表 4.16 的格里森直齿锥齿轮的齿形和表 4.17 的标准直齿锥齿轮的齿形示意于图 4.11。
(2)标准直齿锥齿轮
标准直齿锥齿轮的齿形为全齿高齿, 并且没有变位。计算方法如表4.17。
表4.17 标准直齿锥齿轮的计算| 序号 | 计算项目 | 代号 | 计算方程式 | 计算例 | |
| 小齿轮(1) | 大齿轮(2) | ||||
| 1 | 轴交角 | Σ | 设定值 | 90° | |
| 2 | 大端模数 | m | 3 | ||
| 3 | 分度圆压力角 | α | 20° | ||
| 4 | 齿数 | z | 20 | 40 | |
| 5 | 分度圆直径 | d | zm | 60 | 120 |
| 6 | 分锥角 |
δ1 δ2 |
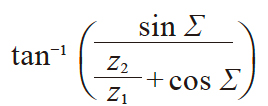
Σ − δ1 |
26.56505° | 63.43495° |
| 7 | 大端锥距 | R |
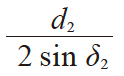
|
67.08204 | |
| 8 | 齿宽 | b | 最好能控制在R / 3 或10 m 以下 | 22 | |
| 9 | 大端齿顶高 | ha | 1.00m | 3.00 | |
| 10 | 大端齿根高 | hf | 1.25m | 3.75 | |
| 11 | 齿根角 | θf | tan−1 ( hf / R ) | 3.19960° | |
| 12 | 齿顶角 | θa | tan−1 ( ha / R ) | 2.56064° | |
| 13 | 顶锥角 | δa | δ + θa | 29.12569° | 65.99559° |
| 14 | 根锥角 | δf | δ − θf | 23.36545° | 60.23535° |
| 15 | 大端齿顶圆直径 | da | d + 2ha cos δ | 65.3666 | 122.6833 |
| 16 | 冠顶距 | X | R cos δ − ha sin δ | 58.6584 | 27.3167 |
| 17 | 齿顶间轴向距 | Xb |
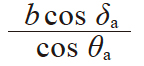
|
19.2374 | 8.9587 |
| 18 | 小端齿顶圆直径 | di |
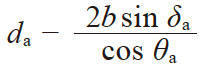
|
43.9292 | 82.4485 |
表4.17 除正交轴外, 也可使用其计算斜交直齿锥齿轮。
(3)格里森弧齿(螺旋齿) 锥齿轮
弧齿锥齿轮如图4.12 所示, 是齿线呈曲线形的锥齿轮。齿线 dc 和节锥母线的夹角为螺旋角。齿面中央的螺旋角为中央螺旋角 βm , 或称为螺旋角。
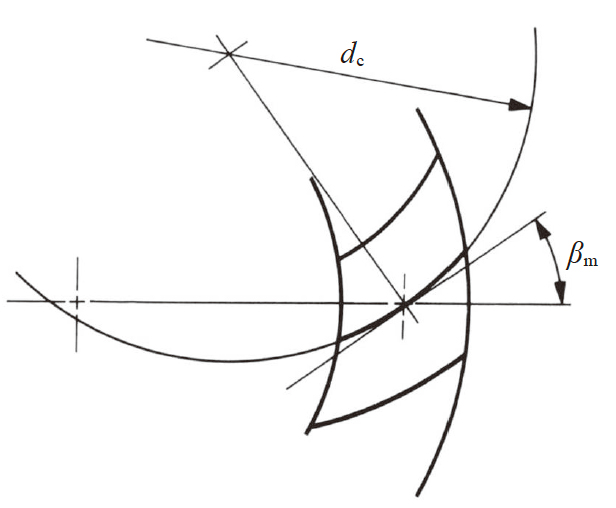
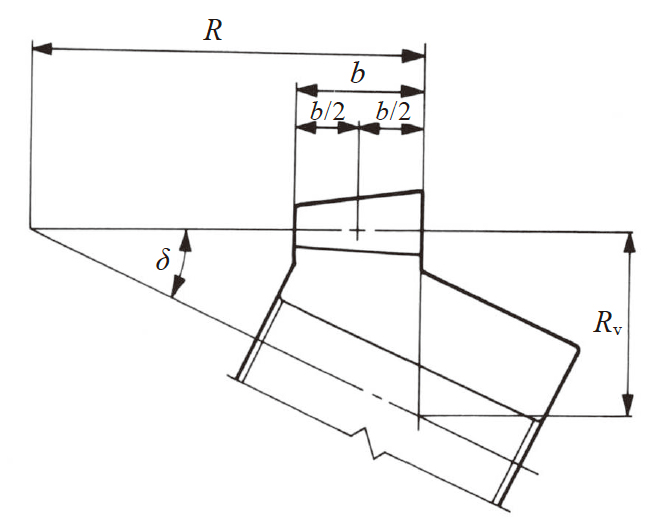
图4.12 弧齿锥齿轮(左旋)
表4.20 所示的格里森弧齿锥齿轮的计算公式是使
用双面切削法及单面铣刀切削法展成加工时的公式。使用不同的方法加工时, 计算公式也不同。
这里所介绍的格里森弧齿锥齿轮的齿形是齿高 h = 1.888m, 顶隙 c = 0.188m, 工作齿高 hw = 1.700m的短齿, 模数2.1 以上的齿轮可以使用。
轴交角 Σ = 90° , 法向压力角 αn = 20°的格里森弧齿锥齿轮, 不发生根切的最小齿数列于表4.18。
| 法向压力角 | 齿数的组合z1 / z2 | |||||
| 20° | 17/17 以上 | 16/18 以上 | 15/19 以上 | 14/20 以上 | 13/22 以上 | 12/26 以上 |
小齿轮的齿数小于12 时, 根据表4.19 来决定齿形的尺寸。
表4.19 小齿轮齿数不超过12 的弧齿锥轮的尺寸|
小齿轮齿数
z1
|
6 | 7 | 8 | 9 | 10 | 11 | |
|
大齿轮齿数
z2
|
34 以上 | 33 以上 | 32 以上 | 31 以上 | 30 以上 | 29 以上 | |
|
工作齿高
hw
|
1.500 | 1.560 | 1.610 | 1.650 | 1.680 | 1.695 | |
|
全齿高
h
|
1.666 | 1.733 | 1.788 | 1.832 | 1.865 | 1.882 | |
|
大齿轮的齿顶高
ha2
|
0.215 | 0.270 | 0.325 | 0.380 | 0.435 | 0.490 | |
|
小齿轮的齿顶高
ha1
|
1.285 | 1.290 | 1.285 | 1.270 | 1.245 | 1.205 | |
| 大齿轮的圆弧齿厚s2 | 30 | 0.911 | 0.957 | 0.975 | 0.997 | 1.023 | 1.053 |
| 40 | 0.803 | 0.818 | 0.837 | 0.860 | 0.888 | 0.948 | |
| 50 | ─ | 0.757 | 0.777 | 0.828 | 0.884 | 0.946 | |
| 60 | ─ | ─ | 0.777 | 0.828 | 0.883 | 0.945 | |
|
法向压力角
αn
|
20° | ||||||
|
螺旋角
β
|
35°~ 40° | ||||||
|
轴交角
Σ
|
90° | ||||||
格里森弧齿锥齿轮的计算列于表4.20。
表4.20 格里森弧齿锥齿轮的计算| 序号 | 计算项目 | 代号 | 计算方程式 | 计算例 | |
| 小齿轮(1) | 大齿轮(2) | ||||
| 1 | 轴交角 | Σ | 设定值 | 90° | |
| 2 | 大端端面模数 | m | 3 | ||
| 3 | 法向压力角 | αn | 20° | ||
| 4 | 中央螺旋角 | βm | 35° | ||
| 5 | 齿数(螺旋方向) | z | 20(L) | 40(R) | |
| 6 | 端面压力角 | αt |
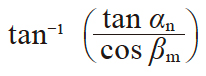
|
23.95680 | |
| 7 | 分度圆直径 | d | zm | 60 | 120 |
| 8 | 分锥角 | δ1 δ2 |
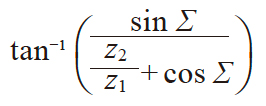
|
26.56505° | 63.43495° |
| 9 | 锥距 | R |
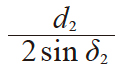
|
67.08204 | |
| 10 | 齿宽 | b | 希望控制在0.3R 或10m 以下 | 20 | |
| 11 | 大端齿顶高 | ha1 ha2 |
1.700m − ha2
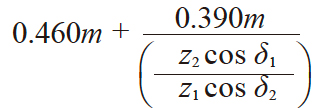
|
3.4275 | 1.6725 |
| 12 | 大端齿根高 | hf | 1.888m − ha | 2.2365 | 3.9915 |
| 13 | 齿根角 | θf | tan−1 ( hf / R ) | 1.90952° | 3.40519° |
| 14 | 齿顶角 | θa1 θa2 |
θf2 θf1 |
3.40519° | 1.90952° |
| 15 | 顶锥角 | δa | δ + θa | 29.97024° | 65.34447° |
| 16 | 根锥角 | δf | δ − θf | 24.65553° | 60.02976° |
| 17 | 大端齿顶圆直径 | da | d + 2ha cos δ | 66.1313 | 121.4959 |
| 18 | 冠顶距 | X | R cos δ − ha sin δ | 58.4672 | 28.5041 |
| 19 | 齿顶间轴向距 | Xb |
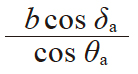
|
17.3563 | 8.3479 |
| 20 | 小端齿顶圆直径 | di |
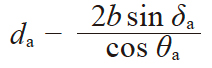
|
46.1140 | 85.1224 |
斜交格里森弧齿齿轮亦可使用表4.20 进行计算。
齿轮副的组合为旋向相反的一对齿轮相配合。
(4)格里森零度锥齿轮
如图4.13 所示, 中央螺旋角 βm 为零的锥齿轮被称为零度锥齿轮。
齿轮的计算与格里森直齿锥齿轮相同, 可以使用表4.16 进行计算。
螺旋方向为左旋与右旋齿相配合使用。图4.13 示意了左旋齿齿轮。
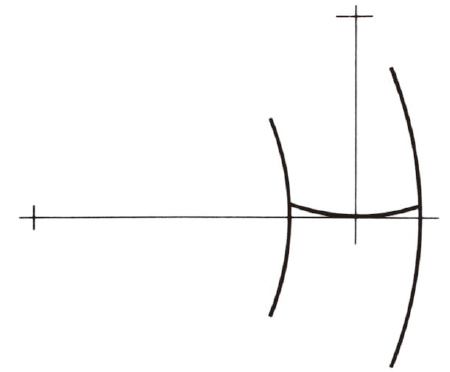
图4.13 零度锥齿轮(左旋齿)
4.5 交错轴斜齿齿轮
交错轴斜齿齿轮是圆柱齿轮( 斜齿齿轮) 副在交错轴间传动时的名称。
交错轴斜齿齿轮本身是斜齿齿轮。
啮合状态示意在图4.14 中。
交错轴斜齿齿轮相互间的法向模数 mn 与法向压力角 αn 须相等才能啮合。
齿轮在无变位情况下啮合时的轴角 Σ 根据分度圆螺旋角 β1、β2 进行计算。

如果将其实行变位, 啮合会变得非常复杂。此时的轴交角 Σ 根据啮合节圆柱螺旋角 βw1、βw2 进行计算。

表4.21 中列出了齿直角方式交错轴变位斜齿齿轮的计算。
计算无变位的标准齿轮时, 计算表中的 xn1 = xn2 = 0 。

图4.14 交错轴斜齿齿轮的啮合
表4.21 齿直角方式变位交错轴斜齿齿轮的计算| 序号 | 计算项目 | 代号 | 计算方程式 | 计算例 | |
| 小齿轮(1) | 大齿轮(2) | ||||
| 1 | 法向模数 | mn | 设定值 | 3 | |
| 2 | 法向压力角 | αn | 20° | ||
| 3 | 分度圆螺旋角 | β | 20° | 30° | |
| 4 | 齿数(螺旋方向) | z | 15(R) | 24(R) | |
| 5 | 法向变位系数 | xn | 0.4 | 0.2 | |
| 6 | 当量齿轮齿数 | zv | z / cos3 β | 18.0773 | 36.9504 |
| 7 | 端面压力角 | αt |
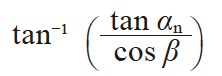
|
21.1728° | 22.7959° |
| 8 | αwn角的渐开线函数 | invαwn |
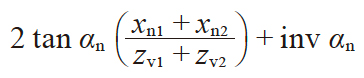
|
0.0228415 | |
| 9 | 法向啮合角 | αwn | 由渐开线函数表中求出 | 22.9338° | |
| 10 | 端面啮合角 | αwt |
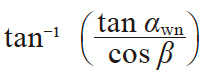
|
24.2404° | 26.0386° |
| 11 | 中心距变动系数 | y |
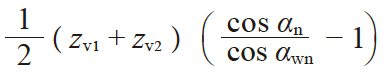
|
0.55977 | |
| 12 | 中心距 | a |
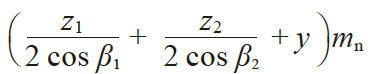
|
67.1925 | |
| 13 | 分度圆直径 | d | zmn / cos β | 47.8880 | 83.1384 |
| 14 | 基圆直径 | db | d cos αt | 44.6553 | 76.6445 |
| 15 | 啮合节径 | dw1 dw2 |
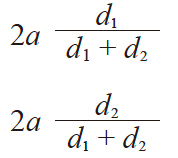
|
49.1155 | 85.2695 |
| 16 | 啮合节圆螺旋角 | βw |
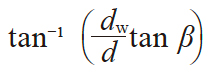
|
20.4706° | 30.6319° |
| 17 | 轴交角 | Σ | βw1 + βw2 或 βw1 − βw2 | 51.1025° | |
| 18 | 齿顶高 | ha1 ha2 |
( 1 + y − xn2 )mn ( 1 + y − xn1 )mn |
4.0793 | 3.4793 |
| 19 | 全齿高 | h | {2.25 + y −( xn1 + xn2 )}mn | 6.6293 | |
| 20 | 齿顶圆直径 | da | d + 2ha | 56.0466 | 90.0970 |
| 21 | 齿根圆直径 | df | da − 2h | 42.7880 | 76.8384 |
无变位的标准交错轴斜齿齿轮的啮合, 如下的关系式成立。
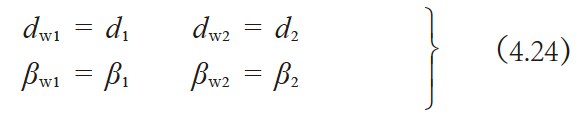
4.6 圆柱蜗杆蜗轮副
圆柱蜗杆蜗轮副是指由拥有螺纹状轮齿的圆柱蜗杆和与之啮合的蜗轮组成的齿轮副。其最常用作交错轴齿轮,一般轴交角为90°。双头以上的蜗杆被称为多头蜗杆。
如图4.15 所示,蜗杆是指具有单头以上轮齿的螺纹状齿轮。在节圆柱上,螺旋线的分度圆柱导程角为γ,每一圈螺旋线对应的导程为pz。

图4.15 圆柱蜗杆(右旋齿)
蜗杆蜗轮为交错轴齿轮,因此蜗杆的轴平面与蜗轮的轴平面不一致。
蜗杆的轴平面为蜗轮的轴直角平面(端平面),蜗杆的轴直角平面(端平面)为蜗轮的轴平面。
唯一一致的平面为法平面。
以该法平面的法向模数 mn 为基准制作蜗杆蜗轮的方法已经非常普及。
根据这种方式,利用市售的齿轮滚刀即可对蜗轮进行切齿加工,非常方便。
蜗杆蜗轮的轴平面、轴直角平面(端平面)和法平面的模数、压力角、齿距及导程的关系如表4.22 所示。
| 蜗杆 | ||
| 轴平面 | 法平面 | 轴直角平面(端平面) |
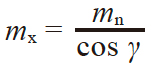
|
mn |
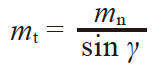
|
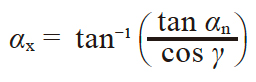
|
αn |
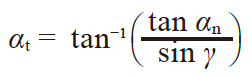
|
| px = πmx | pn = πmn | pt = πmt |
| pz = πmx z |
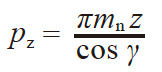
|
pz = πmt z tan γ |
| 轴直角平面(端平面) | 法平面 | 轴平面 |
| 蜗轮 | ||
要理解此表4.22 的关系,可参考图4.15。这些关系式等同于将斜齿齿轮的公式(4.16)、(4.17)中的 β 置换为 90°− γ,因此也可大致认为分度圆柱导程角为γ 的蜗杆是螺旋角为(90°− γ)的斜齿齿轮。
日本工业规格JIS B1723-1977 圆柱蜗轮尺寸中规定的圆柱蜗杆的4 种齿形如图4.16 所示。
JIS1 形是将车刀的直线形切刃安装在轴平面上进行车削加工后的直线轴向齿形。
JIS2 形是将车刀的直线形切刃安装在齿槽直角平面上进行车削加工后的法截面上的直线齿形。
JIS3 形是用轴截面呈梯形的圆盘工具制作而成的凸形轴向齿形。
JIS4 形是将车刀的直线形切刃安装在与轴平面偏移量达到基圆半径的位置上进行车削加工后的渐开线螺纹面齿
形。
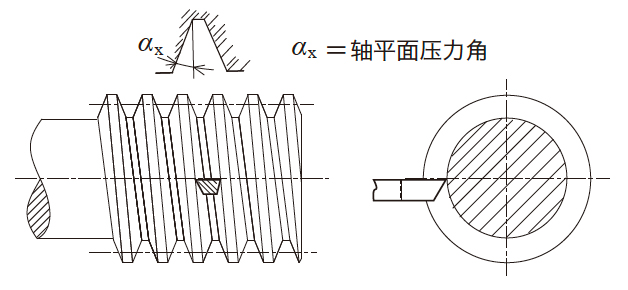
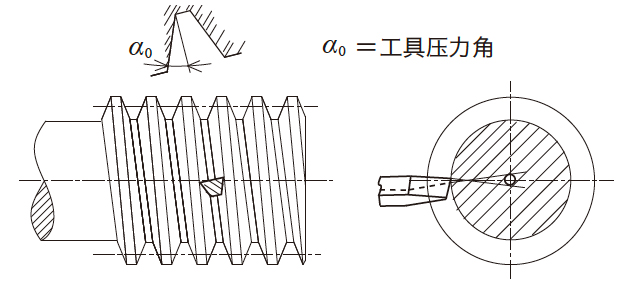
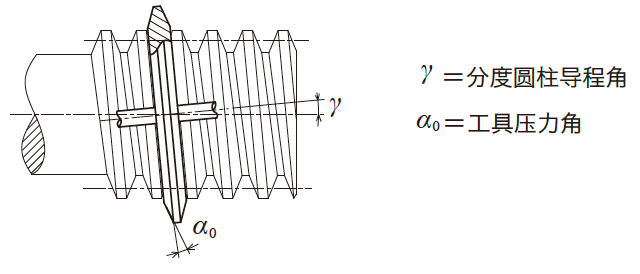
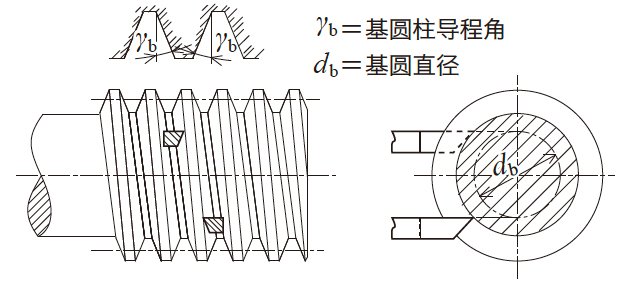
图4.16 JIS 齿形
(1)轴向模数方式蜗杆蜗轮
对于该方式的蜗杆蜗轮,建议以轴向模数 mx、法向压力角 αn =20° 为基准进行齿轮的计算。该计算的详情如表4.23 所示。
表4.23 轴向模数方式蜗杆蜗轮的计算| 编号 | 计算项目 | 符号 | 计算公式 | 计算例 | |
| 蜗杆(1) | 蜗轮(2) | ||||
| 1 | 轴向模数 | mx | 设定值 | 3 | |
| 2 | 法向压力角 | (αn) | (20°) | ||
| 3 | 头数、齿数 | z | 右双头 | 30(R) | |
| 4 | 轴直角变位系数 | xt2 | ─ | 0 | |
| 5 | 分度圆直径 | d1 d2 |
(Qmx) 注1 z2mx |
44.000 | 90.000 |
| 6 | 分度圆柱导程角 | γ |
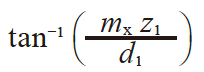
|
7.76517° | |
| 7 | 中心距 | a |
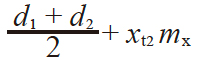
|
67.000 | |
| 8 | 齿顶高 | ha1 ha2 |
1.00 mx (1.00 + xt2)mx |
3.000 | 3.000 |
| 9 | 齿高 | h | 2.25 mx | 6.750 | |
| 10 | 齿顶圆直径 | da1 da2 |
d1 + 2ha1 d2 + 2ha2 + mx 注2 |
50.000 | 99.000 |
| 11 | 喉径 | dt | d2 + 2ha2 | ─ | 96.000 |
| 12 | 喉圆半径 | ri | d1 / 2 − ha1 | ─ | 19.000 |
| 13 | 齿根圆直径 | df1 df2 |
da1 − 2h dt − 2h |
36.500 | 82.500 |
Q = d1 / mx
注2.蜗轮的齿顶圆直径 da2还有很多其它计算公式。注3.蜗杆的齿宽b1 达到 πmx( 4.5 + 0.02z2 )即足够。
注4.蜗轮的有效齿宽 bw 为
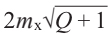 ,因此蜗轮的齿宽 b2 达到 bw + 1.5mx 以上即足够。
,因此蜗轮的齿宽 b2 达到 bw + 1.5mx 以上即足够。
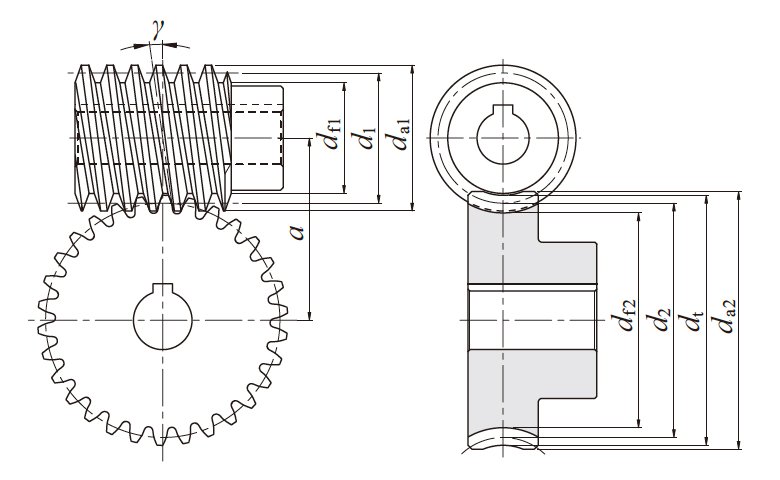
图4.17 圆柱蜗杆蜗轮的尺寸
(2)齿直角方式蜗杆蜗轮
此方式的蜗杆蜗轮以法向模数 mn , 法向齿形角
αn = 20° 为基准进行齿轮的计算。表4.24 为计算表。
| 序号 | 计算项目 | 代号 | 计算方程式 | 计算例 | |
| 蜗杆(1) | 蜗轮(2) | ||||
| 1 | 法向模数 | mn | 设定值 | 3 | |
| 2 | 法向齿形角 | αn | ( 20°) | ||
| 3 | 头数·齿数 | z | 右双头 | 30(R) | |
| 4 | 蜗杆节圆直径 | d1 | 44.000 | ─ | |
| 5 | 法向变位系数 | xn2 | − | − 0.1414 | |
| 6 | 分度圆柱导程角 | γ |
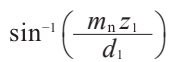
|
7.83748° | |
| 7 | 蜗轮节圆径 | d2 | z2mn / cos γ | ─ | 90.8486 |
| 8 | 中心距 | a |
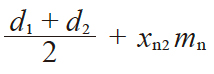
|
67.000 | |
| 9 | 齿顶高 | ha1 ha2 |
1.00 mn (1.00 + xn2) mn |
3.000 | 2.5758 |
| 10 | 全齿高 | h | 2.25 mn | 6.75 | |
| 11 | 齿顶圆直径 | da1 da2 |
d1 + 2ha1 d2 + 2ha2 + mn |
50.000 | 99.000 |
| 12 | 喉径 | dt | d2 + 2ha2 | ─ | 96.000 |
| 13 | 喉圆半径 | ri | d1 / 2 − ha1 | ─ | 19.000 |
| 14 | 齿根圆直径 | df1 df2 |
da1 − 2h dt − 2h |
36.500 | 82.500 |
(3)蜗杆蜗轮的鼓形加工
对于蜗杆蜗轮, 与其他的齿轮相比, 鼓形加工尤为重要。通过鼓形加工, 可以防止因为齿轮的安装误差等引起的片面接触, 确保形成油膜所必须的入口间隙。
鼓形加工的四种方法介绍如下。
对蜗轮的轮齿施行鼓形加工的方法, 有以下几种。
(a)使用比蜗杆的分度圆大的滚刀加工蜗轮
使用与蜗杆同径的滚刀加工蜗轮时, 蜗轮的鼓面加工余量为零。
象这样完全没有误差地被加工出来的蜗轮副, 被无误差地组装后, 齿接触应该是齿面全面重合。这主要有两个问题, 一是入口间隙无法确保, 二是象这样无误差的理想状况是不现实的, 结果终究是成为片面接触。
想解决这些问题, 如图4.18 所示, 使用大分度圆直径的滚刀切削蜗轮, 这样使齿接触集中在齿宽的中央部,入口的间隙得以保证。
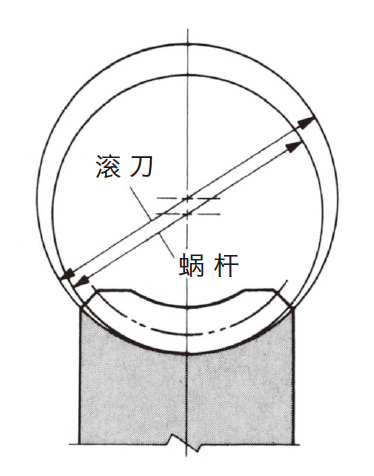
图4.18 使用大直径滚刀的切齿方法
(b)滚刀轴沿齿宽方向上下微量 Δh 移动后切齿的方法
使用滚床对蜗轮进行切齿时, 滚刀轴与蜗轮的中心对位。在这种情况下, 完成通常的全深度切齿后,将滚刀轴的中心向上移动 Δh 量后切齿, 然后按同样的顺序向下移动 Δh 后切齿。因为上下移动时, 沿着齿线进行, 所以需要选择移动方向。一是与导程角相吻合的导程上下移动, 二是将半成品沿圆周方向移动后在上下的位置固定。通过这样的方法达到齿部的鼓形加工目的。
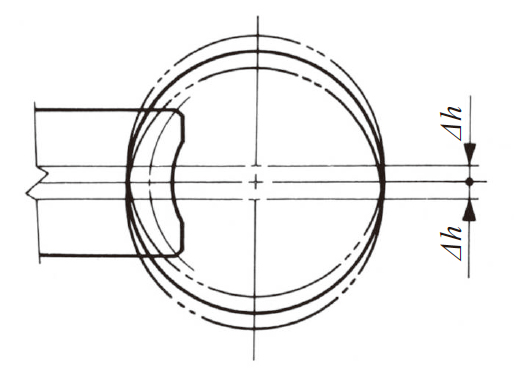
图4.19 上下移动法
(c)滚刀轴左右倾斜 Δθ 角度的切齿方法
利用滚床加工蜗轮轮齿时, 滚刀轴按已经过计算的安装角进行安装后实行通常的切齿加工, 然后将滚刀轴向左倾斜 Δθ 角度, 安装后切齿。按同样顺序向右倾斜后切齿, 这样达到齿面的鼓形加工目的。
以上对蜗轮实行鼓形加工的方法中, 使用最为广泛的是(a) 的方法。(b) 和(c) 很少被使用。
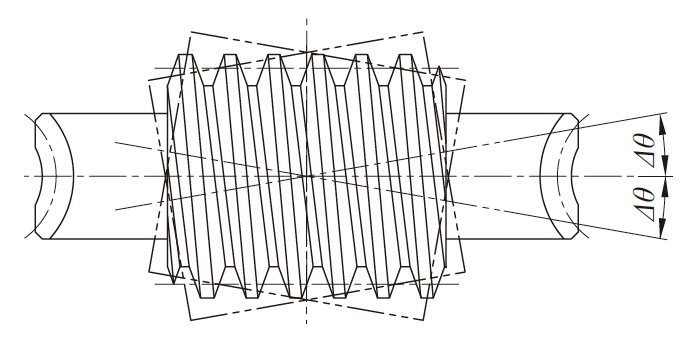
图4.20 左右倾斜法
下面介绍蜗杆的鼓形加工方法。
(d)将蜗杆的轴平面齿形角加工成比蜗轮的轴平面齿形角大以得到蜗杆的鼓形
这个方法可以不改变对于齿轮来说最为重要的轴平面上的基圆齿距, 只改变轴平面齿形角及轴向齿距即可达到蜗杆的鼓形加工目的。
px cos αx = pwx cos αwx(4.25)
修形后的轴平面齿形角αx 比修形前的αwx 增大后,要想满足方程式(4.25), 就必须将修形后的轴向齿距px 也增大。
也就是说, 这种方法是轴平面齿形角αx 和轴向齿距px 增大修形法。
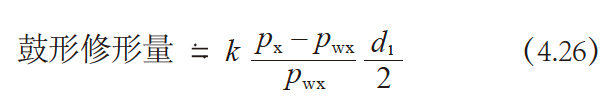
- 其中 d1
- :蜗杆的分度圆直径
- k
- :系数。可以从表4.25 或图4.21 中查出。
| αx | 14.5° | 17.5° | 20° | 22.5° |
| k | 0.55 | 0.46 | 0.41 | 0.375 |
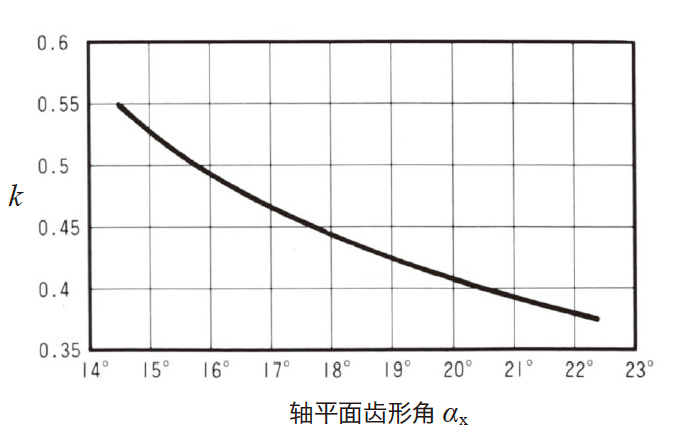
图4.21 系数 k 值
表 4.26 列出了蜗杆的鼓形修形计算。
表4.26 蜗杆的鼓形加工计算| 序号 | 计算项目 | 代号 | 计算方程式 | 计算例 | |
| 1 | 轴向模数 | mwx | 注: 这是修形前的数值。 | 3 | |
| 2 | 法向齿形角 | αwn | 20° | ||
| 3 | 蜗杆的头数 | z1 | 2 | ||
| 4 | 蜗杆的分度圆直径 | d1 | 44.000 | ||
| 5 | 分度圆柱导程角 | γw |
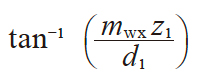
|
7.765166° | |
| 6 | 轴平面齿形角 | αwx |
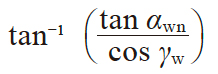
|
20.170236° | |
| 7 | 轴向齿距 | pwx | πmwx | 9.424778 | |
| 8 | 导程 | pwz | πmwxz1 | 18.849556 | |
| 9 | 鼓形修形量 | CR | 根据齿接触的比例来决定 | 0.04 | |
| 10 | 系数 | k | 从表 4.26 中查出 | 0.41 | |
| ※ 修形后的数据 | ||||
| 11 | 轴向齿距 | px |
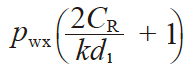
|
9.466573 |
| 12 | 轴平面齿形角 | αx |
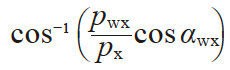
|
20.847973° |
| 13 | 轴向模数 | mx | px / π | 3.013304 |
| 14 | 分度圆柱导程角 | γ |
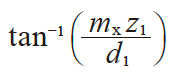
|
7.799179° |
| 15 | 法向齿形角 | αn | tan−1(tanαx cosγ) | 20.671494° |
| 16 | 导程 | pz | πmx z1 | 18.933146 |
(4)蜗杆副的自锁
蜗杆副的特点之一是自锁现象。自锁现象是指由蜗轮无法驱动蜗杆的状态。利用这种特性在升降装置中, 可以简单地保持停止位置等, 其他亦有很多有效的用途。
受各种因素的影响, 蜗杆副有能自锁和不能自锁两种。
轴承损失, 搅拌润滑油损失等完全不产生影响的理想状态下, 自锁现象是否发生的判断取决于齿面的作用力。蜗轮做为驱动齿轮时, 蜗杆的切向力 Ft1 可通过下式计算。
Ft1 = Fn( cos αn sin γ − μ cos γ )(4.27)
切向力 Ft1 大于零时, 不能自锁。从公式中看出, 法向齿形角 αn 分度圆柱导程角 γ 与摩擦系数μ 这三个要素对自锁产生影响。其中静摩擦系数μ 受润滑状况及表面粗糙度等影响, 是不确定要素。
公式(4.27)中, 如果设 Ft1 = 0, αn = 20°的话, 分度圆柱导程角γ 与摩擦系数μ 的关系如图4.23 所示。
实际的蜗杆副中, 摩擦系数 μ 值的正确计算非常的困难。而且, 实际上轴承损失及润滑油搅拌损失等引起的制动力起作用, 要想完全正确地掌握这些要素的作用非常困难。所以, 蜗杆副是否能自锁的判断也就非常的困难。
但是, 可以很确定地断言, 分度圆柱导程角γ 越小,自锁性越高。
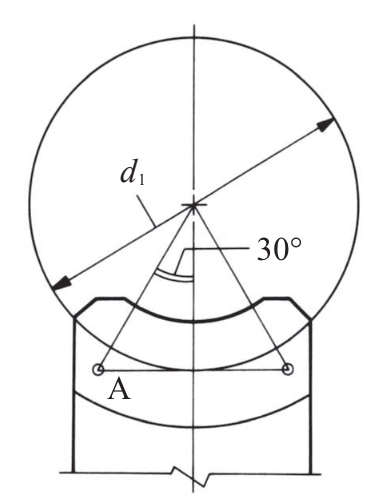
图4.22 计算鼓形修形量的点A
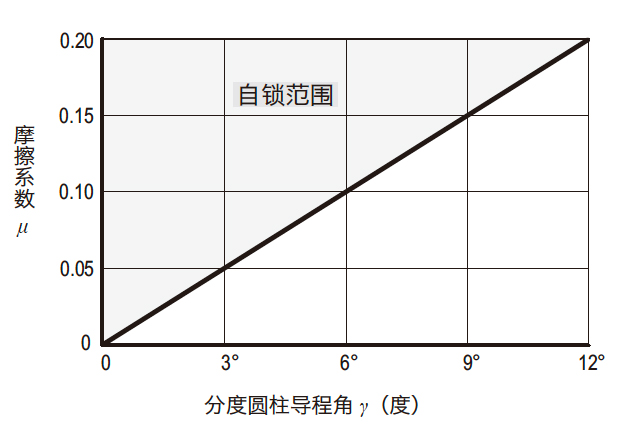
图4.23 分度圆柱导程角 γ 与摩擦系数 μ 的自锁极限


